콘웨이 다면체 표기법
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
콘웨이 다면체 표기법은 다면체의 형태를 변환하는 연산들을 정의하는 방법이다. 이 표기법은 존 호턴 콘웨이가 개발했으며, 기본 연산, 주요 연산, 확장 연산 등으로 구성된다. 기본 연산에는 쌍대(d), 결합(j), 키스(k), 절단(t) 등이 있으며, 확장 연산은 모따기(c), 프로펠러(p) 등이 있다. 또한, 골드버그-콕세터 연산자를 통해 삼각 및 사각형 격자를 기반으로 한 다면체들을 생성할 수 있다. 이 표기법을 통해 아르키메데스 다면체와 카탈랑 다면체를 만들 수 있으며, 평면 및 곡면에서의 테셀레이션에도 적용 가능하다.
더 읽어볼만한 페이지
- 수학 표기법 - 기수법
기수법은 수를 나타내는 방법 또는 체계로, 십진법을 비롯한 다양한 종류가 존재하며, 일진법, 명수법, 위치값 기수법 등으로 분류되고, 가장 널리 사용되는 십진법은 힌두-아라비아 숫자 체계를 기반으로 위치값 기수법의 발전과 0의 도입으로 수학적 계산의 효율성을 높였다. - 수학 표기법 - 중위 표기법
중위 표기법은 사람이 이해하기 쉬운 연산자 표기 방식이지만, 컴퓨터가 구문 분석하기 어렵고 연산 순서를 위해 괄호나 연산자 우선순위 규칙이 필요하다. - 초등 기하학 - 대원
구면기하학에서 대원은 구의 중심을 지나는 평면과 구의 교선으로, 유클리드 공간의 직선에 대응하며, 서로 대극점이 아닌 두 점을 잇는 최단 거리인 대원 거리를 정의하고, 자오선이나 적도처럼 항해, 천문학 등 다양한 분야에서 응용된다. - 초등 기하학 - 현 (기하학)
현은 원 둘레를 두 호로 나누는 선분으로, 원에 내접하는 정다각형의 변이 될 수 있으며, 원의 중심을 지나는 가장 긴 현은 지름이라고 한다. - 다면체 - 마름모구십면체
마름모구십면체는 깎은 정이십면체에 각뿔을 붙여 만든 다면체이며, 넓은 마름모 60개와 좁은 마름모 30개로 구성되고 좁은 마름모는 황금비의 제곱과 관련된 대각선 비율을 가지며 최적 충전율은 약 0.7947이다. - 다면체 - 삼각쌍뿔
삼각쌍뿔은 6개의 정삼각형 면, 5개의 꼭짓점, 9개의 모서리를 가진 존슨 다면체이자 델타다면체로, 두 정사면체를 밑면끼리 결합한 형태이며, 분자 기하학, 색채 이론 등 다양한 분야에 응용된다.
| 콘웨이 다면체 표기법 | |
|---|---|
| 콘웨이 다면체 표기법 | |
| 목적 | 더 높은 차원의 다면체를 묘사하는 방법 |
| 개발자 | 존 호턴 콘웨이 |
| 특징 | 다면체 연산자를 사용하여 다면체를 표현 다면체의 대칭성을 활용 간단하고 직관적인 표기법 |
| 표기법 종류 | tC (Truncate): 모서리를 자름 taC (깎은 자르기): 모서리를 더 깊게 자름 dC (Duality): 쌍대 다면체 oC (Ortho): 정규화 aC (Ambo): 모서리 결합 kC (Kis): 면에 꼭짓점을 추가 mC (Meta): 면을 확장 jC (Join): 면을 결합 gC (Gyro): 회전 sC (Snub): 엇갈린 자르기 eC (Expand): 팽창 pC (Propellor): 프로펠러 rC (Reflect): 반사 bC (Bevel): 모따기 |
| 연산 예시 | |
| t(aC) | 콘웨이 표기법에서 't(aC)'는 'aC' 다면체에 '깎기' 연산을 적용한 것을 의미 |
| dC = O | 쌍대 다면체는 정규화 연산과 동일 |
| aa = e | 두 번의 'a' 연산은 'e' (Expand, 팽창) 연산과 동일 |
| ta = b | 't' 연산 후 'a' 연산을 적용하는 것은 'b' (Bevel, 모따기) 연산과 동일 |
| 응용 | |
| 활용 분야 | 다면체 연구 기하학 교육 컴퓨터 그래픽스 건축 디자인 |
| 참고 자료 | |
| 관련 서적 | The Symmetries of Things (John Conway, Heidi Burgiel, Chaim Goodman-Strauss) |
| 외부 링크 | George W. Hart의 Conway Notation for Polyhedra Adrian Rossiter의 Conway Notation transformations (Antiprism Polyhedron Modelling Software) Anselm Levskaya의 polyHédronisme |
2. 기본 연산
존 호턴 콘웨이가 제시하지는 않았지만, 쌍대성에 의해 콘웨이 연산과 관련이 있는 시드(S), 니들(n), 지퍼(z) 연산도 기본 연산에 포함된다. 콘웨이 다면체 표기법의 기본 연산은 다면체의 형태를 변환하는 간단한 작업들이다.
연산은 정육면체 씨앗(seed)을 기준으로 시각화할 수 있다. 정육면체의 표면에 그려진 파란색 면은 씨앗의 모서리를 가로지르고, 분홍색 면은 씨앗의 꼭짓점에 놓인다. 특히 카이랄 연산자의 경우 꼭짓점 배치에 유연성이 있다.
콘웨이 표기법에서 다면체 연산자는 함수처럼 오른쪽에서 왼쪽으로 적용된다. 예를 들어, 육팔면체는 'ambo cube' [6], 즉 aC영어이고, 깎은 육팔면체는 taC영어이다. 연산자를 반복 적용하는 것은 지수로 나타낼 수 있다. 즉, ''j2'' = ''o''이다. 일반적으로 콘웨이 연산자는 교환 법칙이 성립하지 않는다.
개별 연산자는 기본 영역(또는 챔버) 측면에서 시각화할 수 있다. 각 직각 삼각형은 기본 영역이다. 각 흰색 챔버는 다른 챔버의 회전된 버전이며, 각 색상 챔버도 마찬가지이다. 비대칭 연산자의 경우 색상 챔버는 흰색 챔버의 반사이며, 모두 전이적이다. 그룹 측면에서 비대칭 연산자는 면의 변의 수가 ''n''인 이면체군에 해당하고, 대칭 연산을 하지 않는 대칭군인 순환군에 해당한다. 비대칭 및 대칭 연산자는 각각 국소 대칭 보존 연산(LSP) 및 방향 보존 대칭을 보존하는 국소 연산(LOPSP)이라고도 한다.[7][8][9]
LSP는 국소 대칭을 보존하는 연산이 아니라 대칭을 보존하는 국소 연산으로 이해해야 한다. 다시 말하지만, 이것은 기하학적 의미가 아닌 위상학적 의미의 대칭이다. 즉, 정확한 각도와 모서리 길이는 다를 수 있다.
| 3 (삼각형) | 4 (정사각형) | 5 (오각형) | 6 (육각형) |
|---|---|---|---|
 |  |  |  |
| 다면체 그룹의 기본 영역. 그룹은 비대칭 다면체의 경우 이고, 대칭 다면체의 경우 이다. | |||
Hart는 다면체의 거울상을 제공하는 반사 연산자 ''r''을 도입했다.[6] 이는 방향을 보존하지 않으므로 엄밀히 말하면 LOPSP가 아니다. 흰색 챔버와 빨간색 챔버를 교환하여 방향을 반전한다. ''r''은 방향 외에는 비대칭 다면체에 영향을 미치지 않으며, ''rr = S''는 원래의 다면체를 반환한다. 오버라인은 연산자의 다른 대칭 형태를 나타내는 데 사용할 수 있다. 즉, = ''rsr''이다.
연산이 ''d'' 및 ''r'' 이외의 연산의 조합으로 표현할 수 없는 경우, 이를 기약 연산이라고 한다. 콘웨이의 원래 연산자의 대부분은 기약 연산이다. 예외는 ''e'', ''b'', ''o'' 및 ''m''이다.
2. 1. 주요 연산
존 호턴 콘웨이가 제안한 연산자 외에 추가적인 연산자가 존재한다. 주요 연산자는 다음과 같다.[6]| 가장자리 계수 | 행렬 | x | xd | dx | dxd | 비고 |
|---|---|---|---|---|---|---|
| 1 | 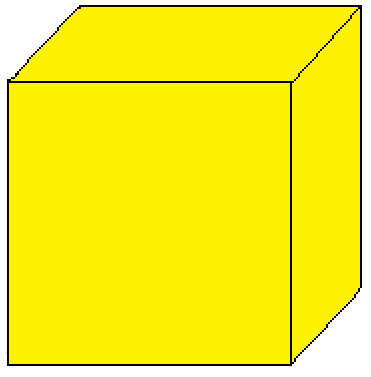 씨앗: S | 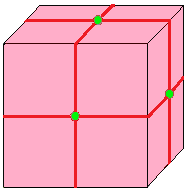 쌍대: d | -- 씨앗: dd = S | 쌍대는 각 면을 꼭짓점으로, 각 꼭짓점을 면으로 바꾼다. | ||
| 2 | 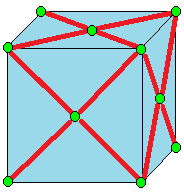 결합: j | 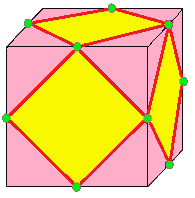 엠보: a | 결합은 사각형 면을 만든다. 엠보는 차수-4 꼭짓점을 생성하며, 정사각형화 또는 그래프 이론에서 중간 그래프라고도 한다.[10] | |||
| 3 | 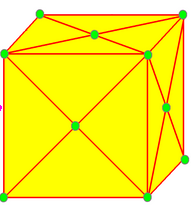 키스: k | 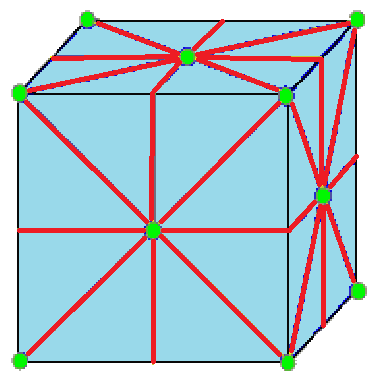 니들: n | 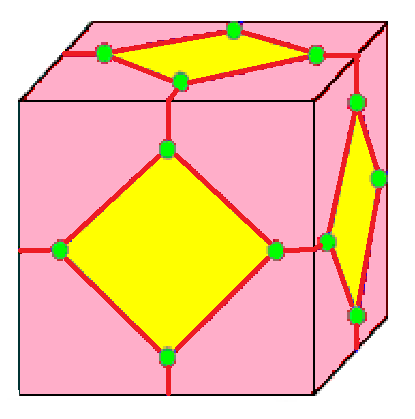 지퍼: z | 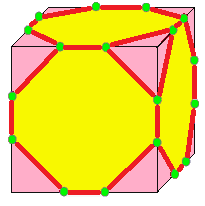 절단: t | 키스는 각 면에 피라미드를 세우며, 아키세이션(akisation), Kleetope, 축적,[11] 부착, 또는 피라미드-증가라고도 한다. 절단은 다면체의 꼭짓점을 잘라내지만 원래 모서리의 일부를 남긴다.[12] 지퍼는 이중절단이라고도 한다. | |
| 4 | 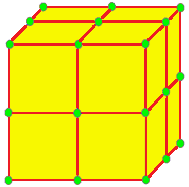 직교: o = jj | 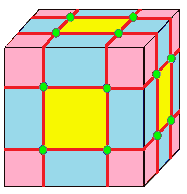 확장: e = aa | ||||
| 5 | 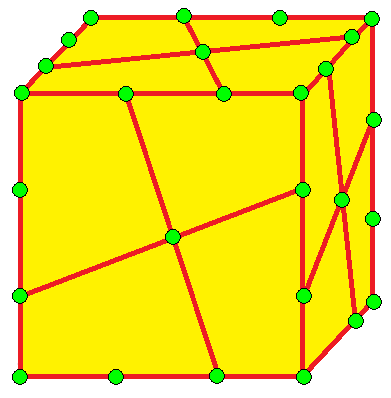 자이로: g | gd = rgr | sd = rsr | 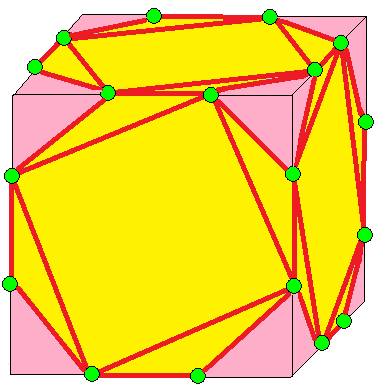 스너브: s | 카이랄 연산자. 스너브 (기하학) 참조. Hart[3]와 반대로, gd는 g와 동일하지 않다. 즉, 카이랄 쌍이다.[13] | |
| 6 | 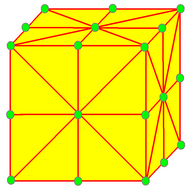 메타: m = kj | 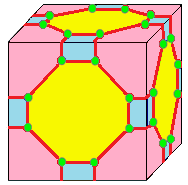 베벨: b = ta | ||||
2. 2. 확장 연산
콘웨이 다면체 표기법에서 확장 연산은 기존 다면체에 새로운 면이나 꼭짓점을 추가하여 더 복잡한 다면체를 만드는 연산이다. 이 연산들은 콘웨이의 원래 연산 집합 이후에 추가되었으며, 다양한 종류가 존재한다.| 모서리 인자 | x | xd | dx | dxd | 비고 |
|---|---|---|---|---|---|
| 4 | 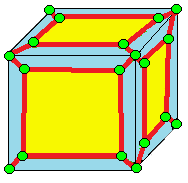 모따기: c | 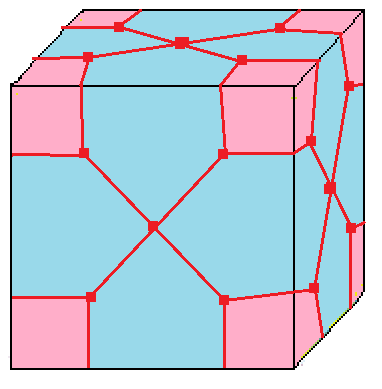 cd = du | 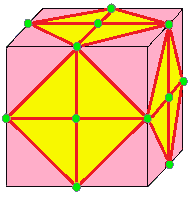 dc = ud | 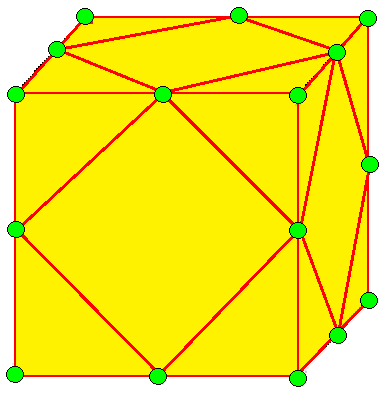 분할: u | 모따기는 l의 결합 형태이다. 모따기 (기하학)를 참조하라. |
| 5 | 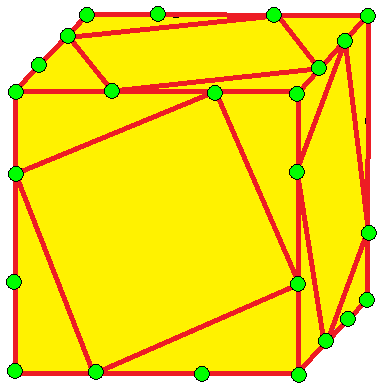 프로펠러: p | 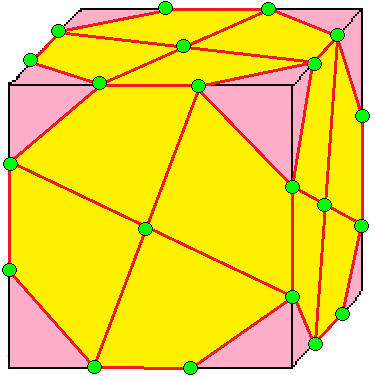 dp = pd | -- dpd = p | 카이랄 연산자. 프로펠러 연산자는 조지 하트에 의해 개발되었다. | |
| 5 | 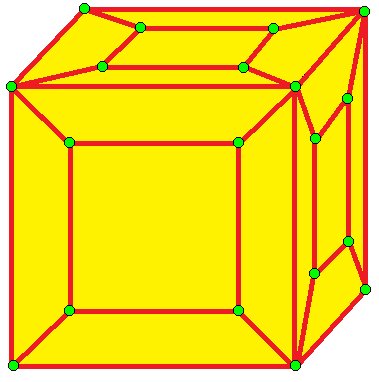 로프트: l | 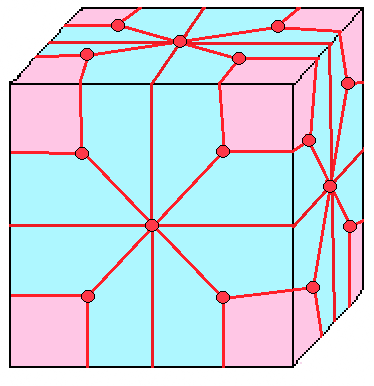 ld | 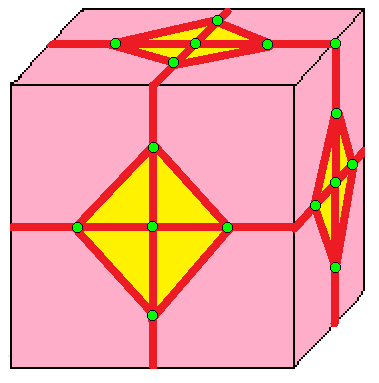 dl | 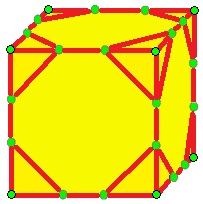 dld | |
| 6 | 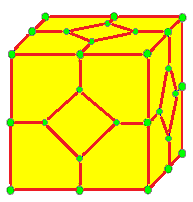 퀸토: q | 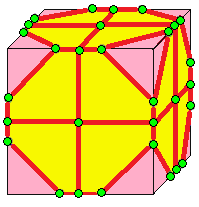 qd | 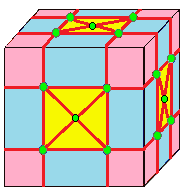 dq | 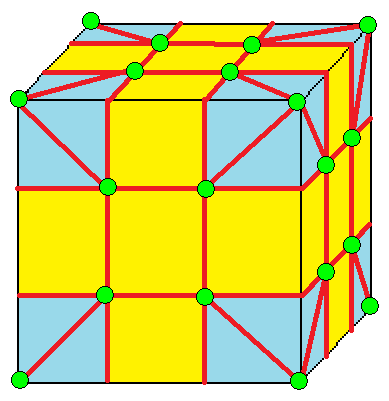 dqd | |
| 6 | 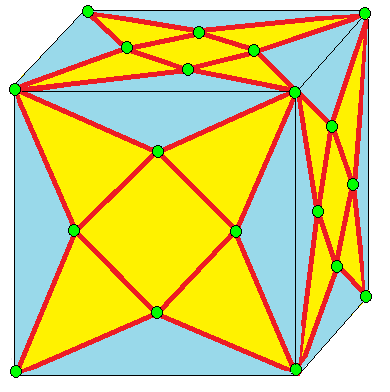 결합-레이스: L0 | 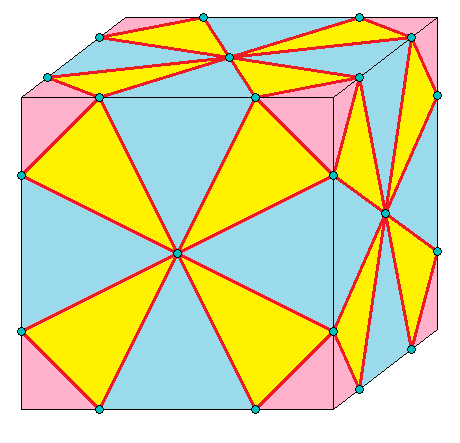 L0d | 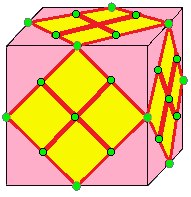 dL0 | 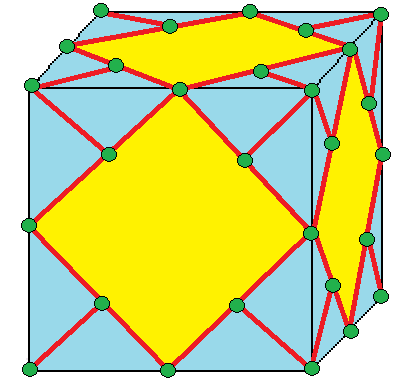 dL0d | 결합 표기법에 대한 설명은 아래를 참조하라. |
| 7 | 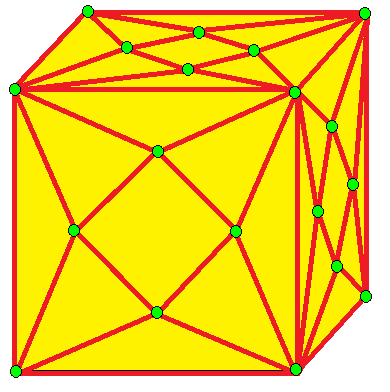 레이스: L | 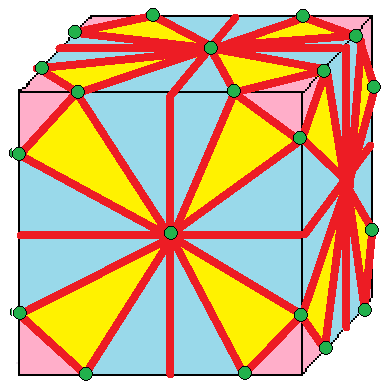 Ld | 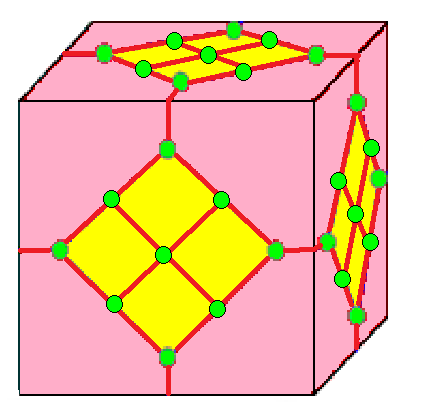 dL | 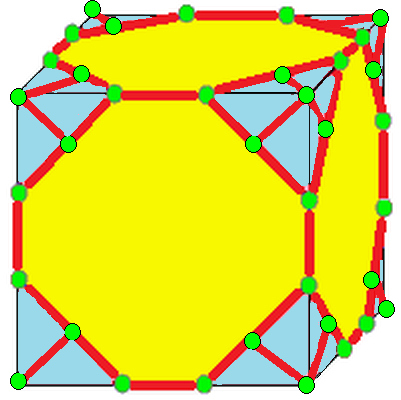 dLd | |
| 7 | 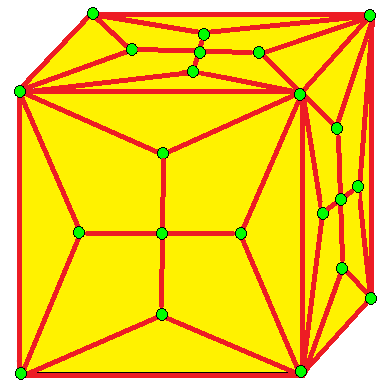 말뚝: K | 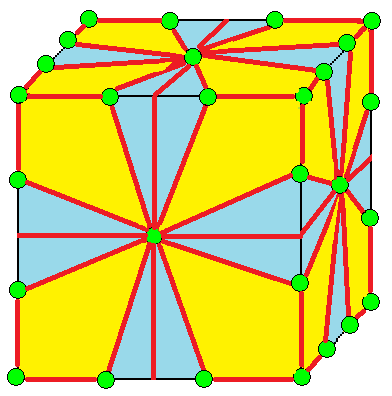 Kd | 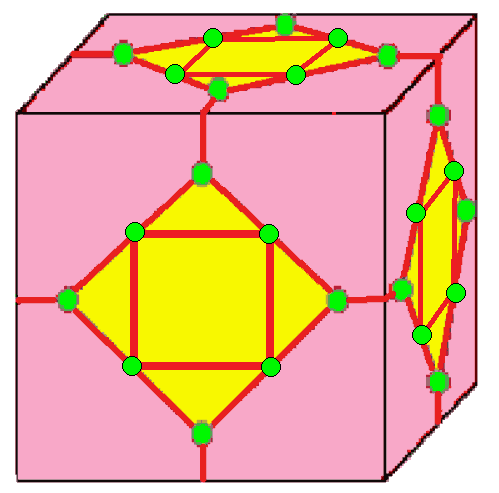 dK | 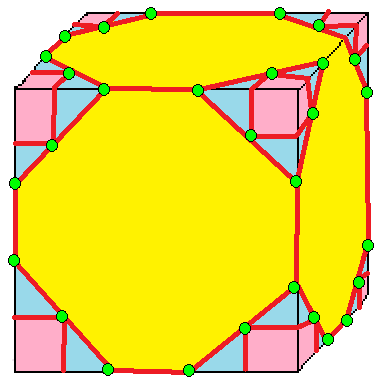 dKd | |
| 7 | 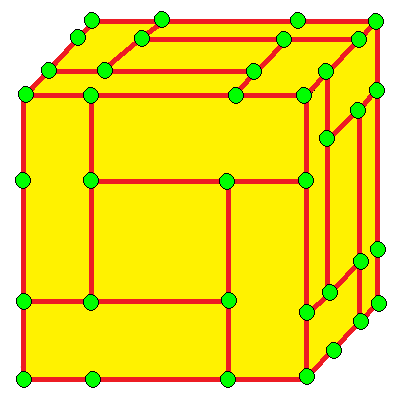 와류: w | wd = dv | 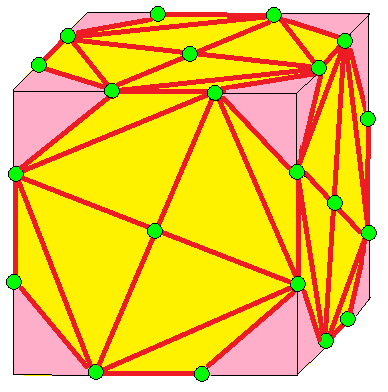 vd = dw | 소용돌이: v | 카이랄 연산자. |
| 8 | 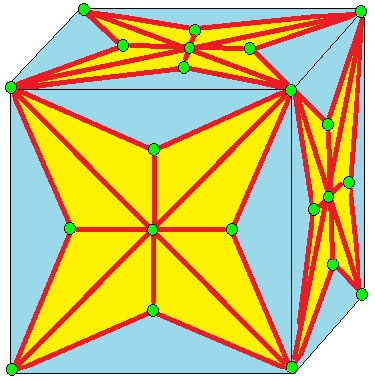 결합-키스-키스: (kk)0 | 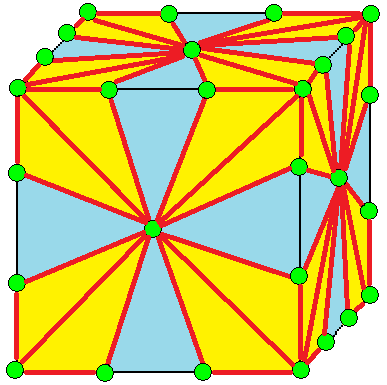 (kk)0d | 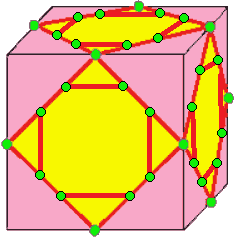 d(kk)0 | 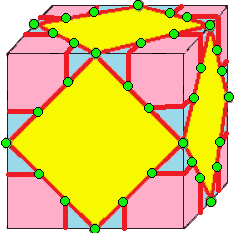 d(kk)0d | 때로는 J로도 불린다. 결합 표기법에 대한 설명은 아래를 참조하라. 비결합 형태, kk는 기약적이지 않다. |
| 10 | 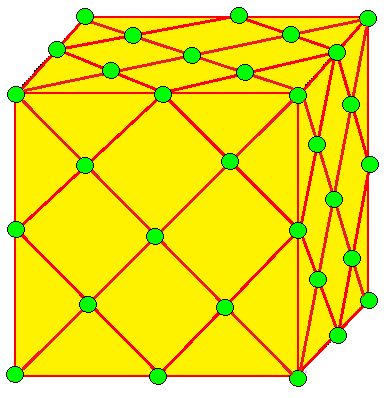 십자: X | 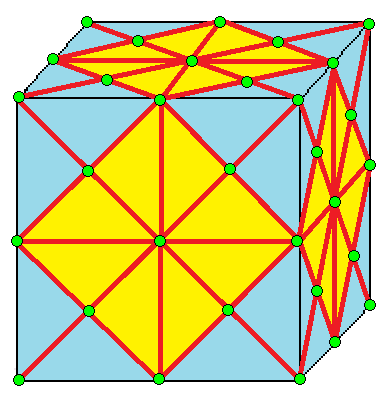 Xd | 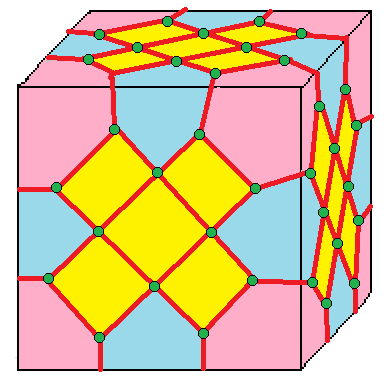 dX | 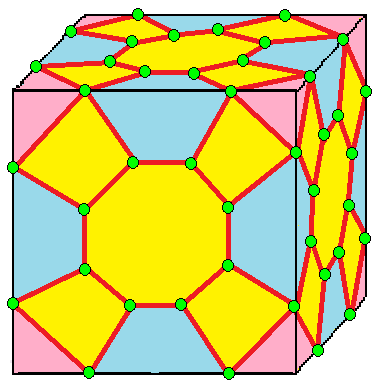 dXd | |
각 연산은 특정한 방식으로 다면체를 변형시킨다. 예를 들어:
- 모따기 (chamfer, c): 모서리를 깎아 육각형 면을 만든다.
- 프로펠러 (propeller, p): 다면체의 면을 오각형으로 분할하고, 각 오각형을 비틀어 새로운 다면체를 만든다. 이 연산은 조지 하트가 개발했으며, 카이랄 연산자이다.
- 로프트 (loft, l)
- 퀸토 (quinto, q)
- 결합-레이스 (Join-lace, L0)
- 레이스 (lace, L)
- 말뚝 (stake, K)
- 와류 (whirl, w): 카이랄 연산자이다.
- 소용돌이 (volute, v)
- 결합-키스-키스 (Join-kis-kis, (kk)0): 때로는 J로도 불린다.
이 외에도 다양한 확장 연산이 존재하며, 이들을 조합하여 더욱 복잡한 다면체를 만들 수 있다.
3. 인덱싱된 확장 연산
몇몇 연산은 특정 기준에 따라 그룹화되거나 지수에 의해 동작이 수정될 수 있다.[8][4] 이는 ''xn''과 같이 아래첨자를 사용하여 연산자 형태로 표기한다.
각 팽창률에 대한 LSP의 수는 팽창률 1부터 시작하여 2, 2, 4, 6, 6, 20, 28, 58, 82, ... 순서로 증가한다. 그러나 모든 LSP가 반드시 모서리와 꼭짓점이 3-연결 그래프를 형성하는 다면체를 생성하는 것은 아니며, 슈타이니츠 정리에 따라 반드시 볼록 시드로부터 볼록 다면체를 생성하는 것도 아니다. 각 팽창률에 대한 3-연결 LSP의 수는 2, 2, 4, 6, 4, 20, 20, 54, 64, ... 순서로 증가한다.[8]
3. 1. 증강 (Augmentation)
증강 연산은 원래의 가장자리를 유지한다. 증강 연산은 면의 독립적인 부분 집합에 적용될 수 있으며, 원래의 가장자리를 제거하여 "결합" 형태로 변환될 수도 있다. 콘웨이 표기법은 이러한 연산자에 선택적 지수를 지원한다. 즉, 결합 형태의 경우 0, 영향을 받는 면의 변이 몇 개인지에 따라 3 이상이다. 예를 들어, ''k''4''Y''4=O: 정사각형 기반 피라미드를 가져와 다른 피라미드를 정사각형 밑면에 붙이면 팔면체가 된다.| 증강 연산자 | x | -- | -- | -- | -- | 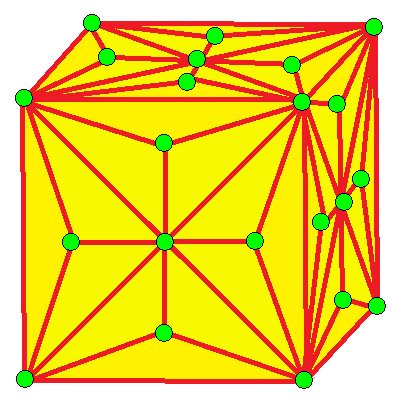 |
|---|---|---|---|---|---|---|
| 해당하는 결합 형태 연산자 | x0 | -- k0 = j | -- l0 = c | -- L0 | 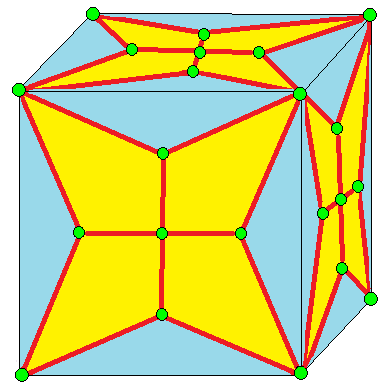 K0 = jk | -- (kk)0 |
| 증강 | 피라미드 | 프리즘 | 각기둥 |
3. 2. 메타/비벨 (Meta/Bevel)
메타는 가운데와 가장자리를 따라 꼭짓점을 추가하고, 베벨은 가운데, 시드 꼭짓점, 가장자리를 따라 면을 추가한다. 지수는 모서리를 따라 추가되는 꼭짓점 또는 면의 수를 나타낸다. 메타(비지수 형태)는 칸티절단 또는 옴니절단이라고도 한다. 여기서 0은 확대 연산과 같은 것을 의미하지 않으며, 모서리를 따라 0개의 꼭짓점(또는 면)이 추가됨을 의미한다.[4]| n | 모서리 계수 | 행렬 | x | xd | dx | dxd |
|---|---|---|---|---|---|---|
| 0 | 3 | -- k = m0 | -- n | -- z = b0 | -- t | |
| 1 | 6 | -- m = m1 = kj | -- b = b1 = ta | |||
| 2 | 9 | 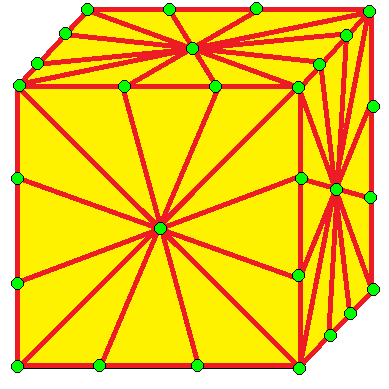 m2 | 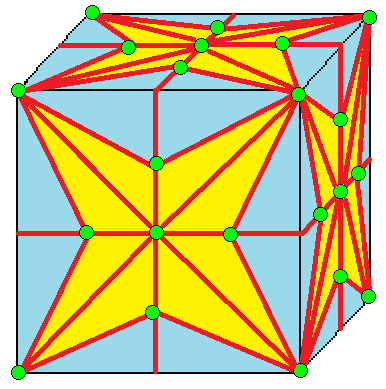 m2d | 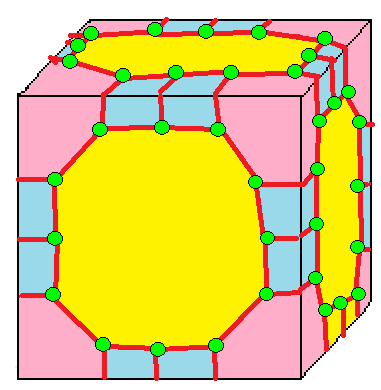 b2 | 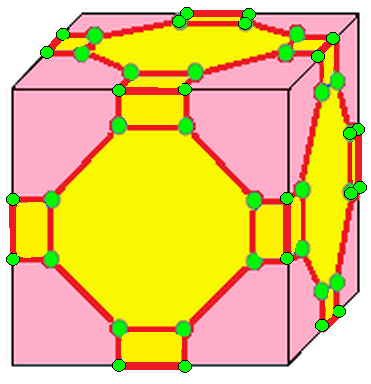 b2d | |
| 3 | 12 | 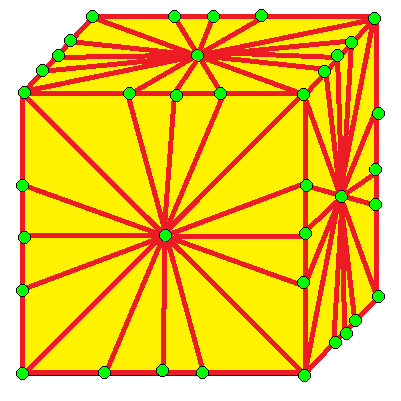 m3 | m3d | b3 | b3d | |
| n | 3n+3 | mn | mnd | bn | bnd | |
메디얼(Medial)은 메타와 유사하지만, 각 시드 꼭짓점의 중심에서 모서리를 추가하지 않는다는 점이 다르다. 인덱스 1 형태는 콘웨이의 오쏘(ortho) 연산자 및 익스팬드(expand) 연산자와 동일하다. 익스팬드는 캔틸레이션 및 확장이라고도 한다. 또한 ''o''와 ''e''는 자체 인덱스 형태를 가지며, 이에 대해서는 아래에 설명한다. 또한 일부 구현에서는 1이 아닌 0부터 인덱싱을 시작한다는 점에 유의해야 한다.[4]
| n | 모서리 계수 | 행렬 | x | xd | dx | dxd |
|---|---|---|---|---|---|---|
| 1 | 4 | -- M1 = o = jj | -- e = aa | |||
| 2 | 7 | 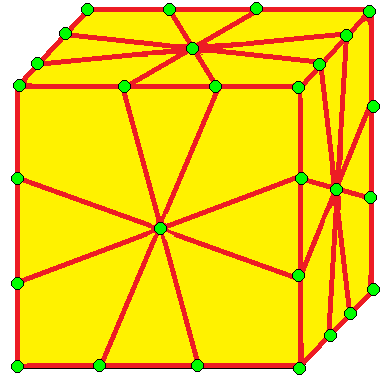 메디얼(Medial): M = M2 | 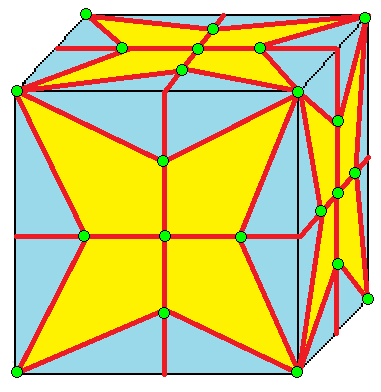 Md | 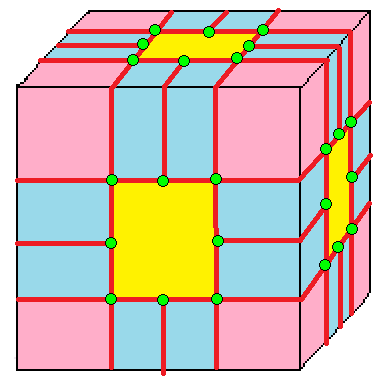 dM | 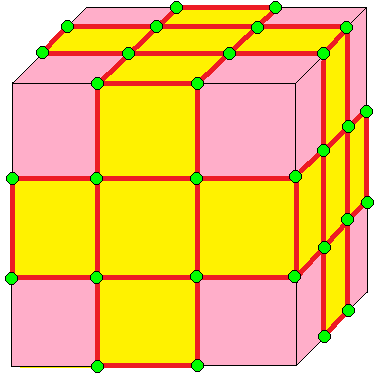 dMd | |
| n | 3n+1 | Mn | Mnd | dMn | dMnd | |
3. 3. 메디알 (Medial)
메디알(Medial)은 메타와 유사하지만, 각 시드 꼭짓점의 중심에서 모서리를 추가하지 않는다는 점이 다르다.[4] 인덱스 1 형태는 콘웨이의 오쏘(ortho) 연산자와 익스팬드(expand) 연산자와 동일하다.[4] 익스팬드는 캔틸레이션 및 확장이라고도 한다.[4] ''o''와 ''e''는 자체 인덱스 형태를 가지며, 이에 대해서는 아래에 설명한다.[4] 일부 구현에서는 1이 아닌 0부터 인덱싱을 시작한다는 점에 유의해야 한다.[4]| n | 모서리 계수 | 행렬 | x | xd | dx | dxd |
|---|---|---|---|---|---|---|
| 1 | 4 | -- M1 = o = jj | -- e = aa | |||
| 2 | 7 | 메디얼(Medial): M = M2 | Md | dM | dMd | |
| n | 3n+1 | Mn | Mnd | dMn | dMnd | |
4. 골드버그-콕시터 연산 (Goldberg-Coxeter)
골드버그-콕세터(Goldberg-Coxeter, GC) 콘웨이 연산자는 골드버그-콕세터 구성을 확장한 두 개의 무한 연산자 집합이다.[16][17] GC 구성은 삼각 격자의 삼각 단면 또는 사각 격자의 사각 단면을 취하여 다면체의 각 면 위에 놓는 것으로 생각할 수 있다. 이 구성은 삼각형 또는 사각형("마스터 다각형")의 챔버를 식별하여 모든 면으로 확장할 수 있다.[7] 삼각 계열의 연산자는 골드버그 다면체와 측지 다면체를 생성하는 데 사용될 수 있으며, 공식은 측지 다면체 및 골드버그 다면체의 목록을 참조하면 된다.
두 계열은 삼각 GC 계열 ''ca,b'' 와 ''ua,b'', 사변형 GC 계열 ''ea,b'' 와 ''oa,b''이다. 두 GC 계열 모두 두 정수 a, b (a≥1, b≥0)로 인덱싱된다. 이들은 다음과 같은 특징을 갖는다.
- 계열의 인덱스는 복소수에 대한 특정 유클리드 정역과 관련이 있다. 삼각 GC 계열은 아이젠슈타인 정수, 사변형 GC 계열은 가우스 정수와 관련된다.
- 동일한 계열 내의 'x' 열과 'dxd' 열의 연산자는 서로 교환 법칙이 성립(통근)한다.
연산자는 세 가지 클래스로 나뉜다(예시는 ''c''를 사용하여 작성되었지만 4개의 연산자 모두에 적용된다).
- 클래스 I: b=0 인 경우이다. 비대칭이며, 원래 모서리를 보존한다. 0 인덱스를 생략하여, 예를 들어 ''c''''a'',0 = ''ca''로 쓸 수 있다.
- 클래스 II: a=b 인 경우이다. 또한 비대칭이며, ''ca,a'' = ''cac''1,1로 분해할 수 있다.
- 클래스 III: a, b 가 0 이 아니고, a 와 b 가 같지 않은 경우를 말한다. 이들은 카이랄이며, ''ca,b'' 와 ''cb,a''는 서로의 카이랄 쌍이다.
원래 콘웨이 연산자 중 GC 계열에 속하지 않는 유일한 연산자는 ''g''와 ''s''(자이로 및 스너브)이다. 메타와 베벨(''m'' 및 ''b'')은 삼각 계열의 하나의 연산자와 사변형 계열의 하나의 연산자로 표현할 수 있다.
기본적인 정수론에 따르면, ''a''와 ''b''의 어떤 값에 대해서도 T = a2 + ab + b2 일 때, 이다.
4. 1. 삼각형 계열 (Triangular)
삼각형 GC 계열은 ''ca,b''와 ''ua,b'' 두 가지 연산자로 구성된다. 이 연산자들은 골드버그 다면체와 측지선 다면체를 만드는 데 사용될 수 있다.두 연산자는 a와 b, 두 정수로 표현되며 a, b의 값에 따라서 연산자의 여러 가지 특징들이 나타난다.
- ''ca,b'' 연산자는 정다면체의 각 면을 정삼각형 격자로 세분화하여 새로운 다면체를 생성한다.
- ''ua,b'' 연산자는 ''ca,b'' 연산자와 유사하지만, 다른 방식으로 정삼각형 격자를 세분화한다.
이 연산자들은 3가지 등급으로 구분된다.
- 클래스 I: 아키랄(achiral)이며, 원래 가장자리를 보존한다. (''ca,0'' = ''ca'')
- 클래스 II: 아키랄(achiral)이며, ''ca,a'' = ''cca1,1''로 분해할 수 있다.
- 클래스 III: 키랄(chiral)쌍을 가지며, ''ca,b''와 ''cb,a''는 서로 거울상 대칭이다.
다음 표는 삼각형 GC 계열 연산자의 예시를 보여준다.
| a | b | 종류 | 모서리 계수 T = a2 + ab + b2 | x | xd | dx | dxd |
|---|---|---|---|---|---|---|---|
| 1 | 0 | I | 1 | -- u1 = S | -- d | -- c1 = S | |
| 2 | 0 | I | 4 | -- u2 = u | -- dc | -- du | -- c2 = c |
| 3 | 0 | I | 9 | 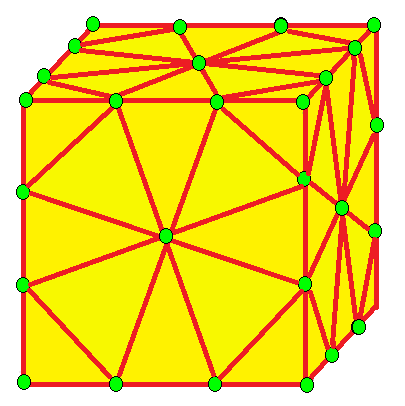 u3 = nn | 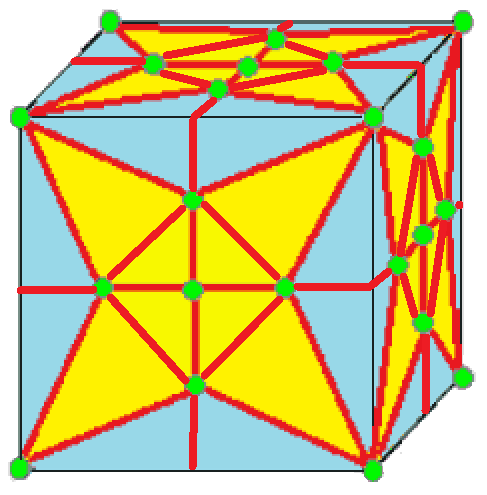 nk | 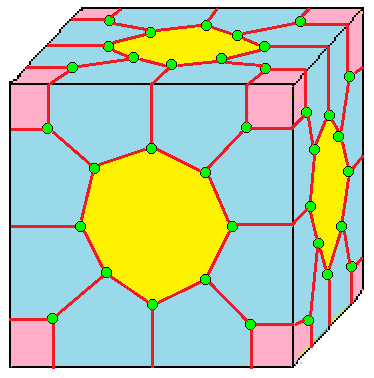 zt | 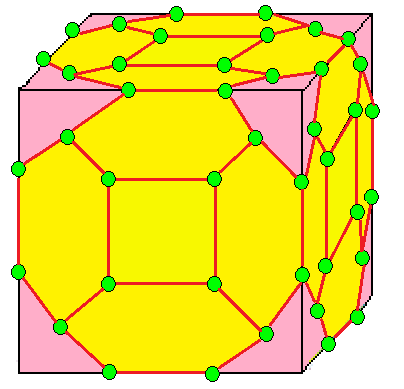 c3 = zz |
| 4 | 0 | I | 16 | 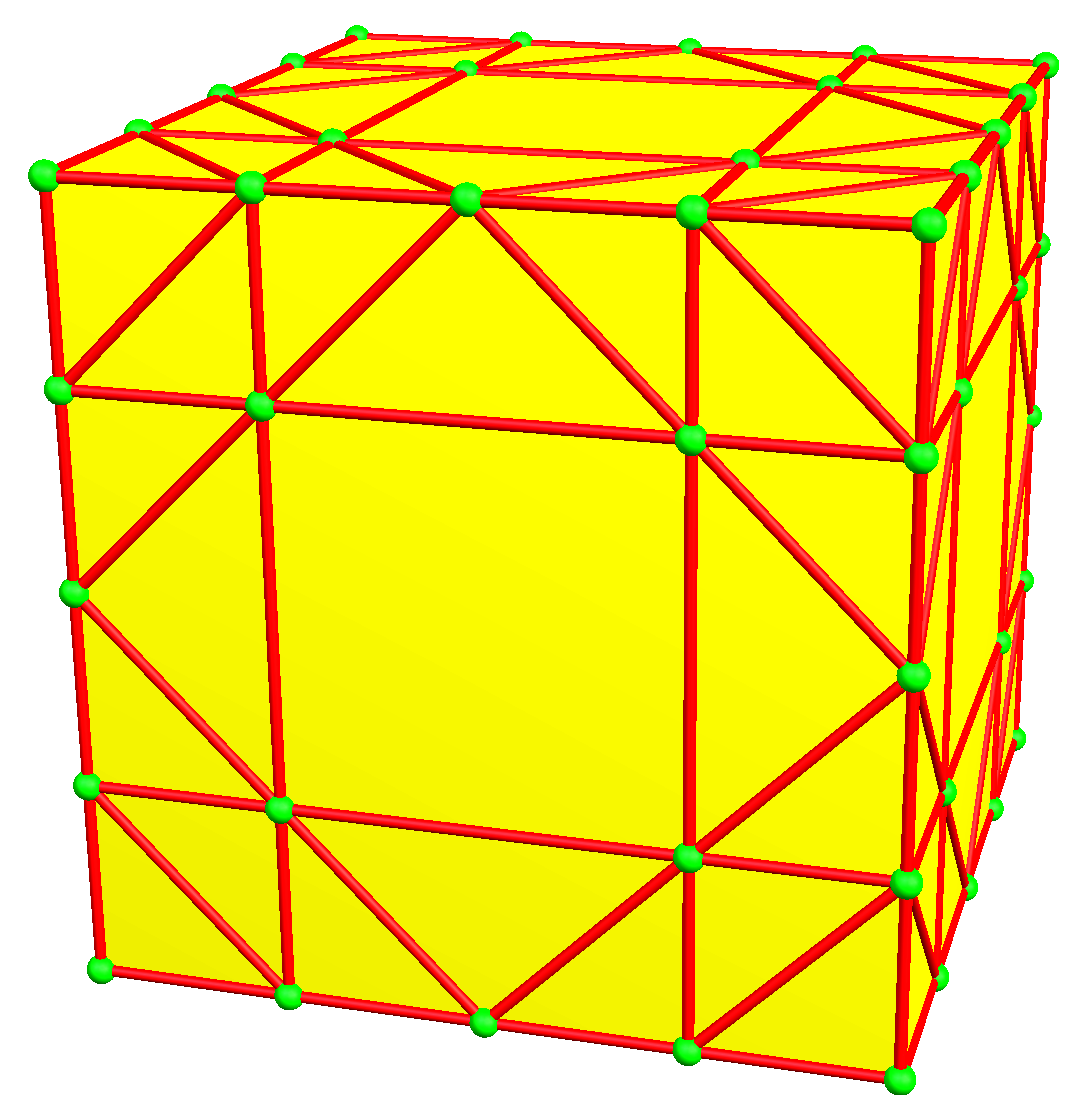 u4 = uu | uud = dcc | duu = ccd | c4 = cc |
| 5 | 0 | I | 25 | 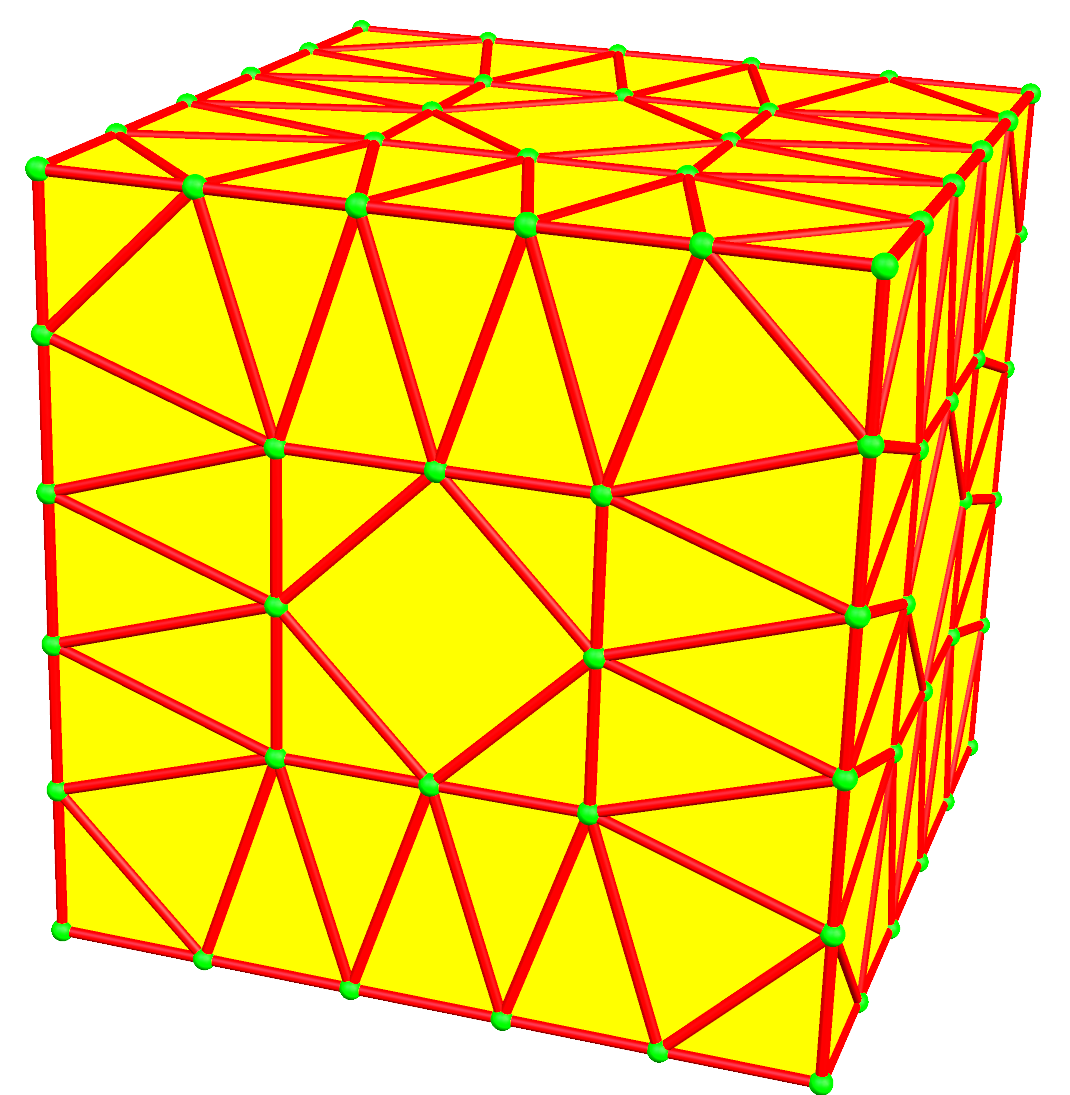 u5 | u5d = dc5 | du5 = c5d | c5 |
| 6 | 0 | I | 36 | 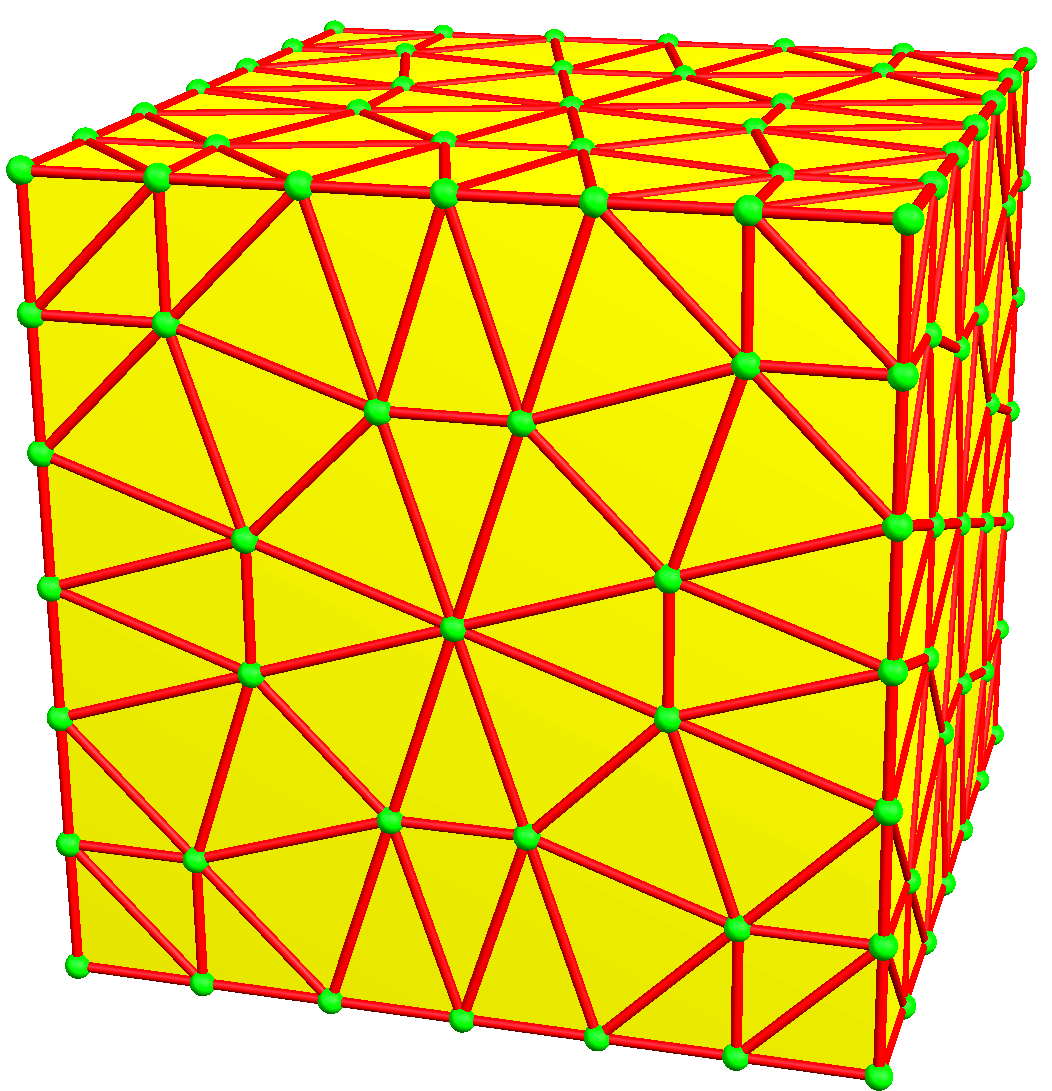 u6 = unn | unk | czt | u6 = czz |
| 7 | 0 | I | 49 | 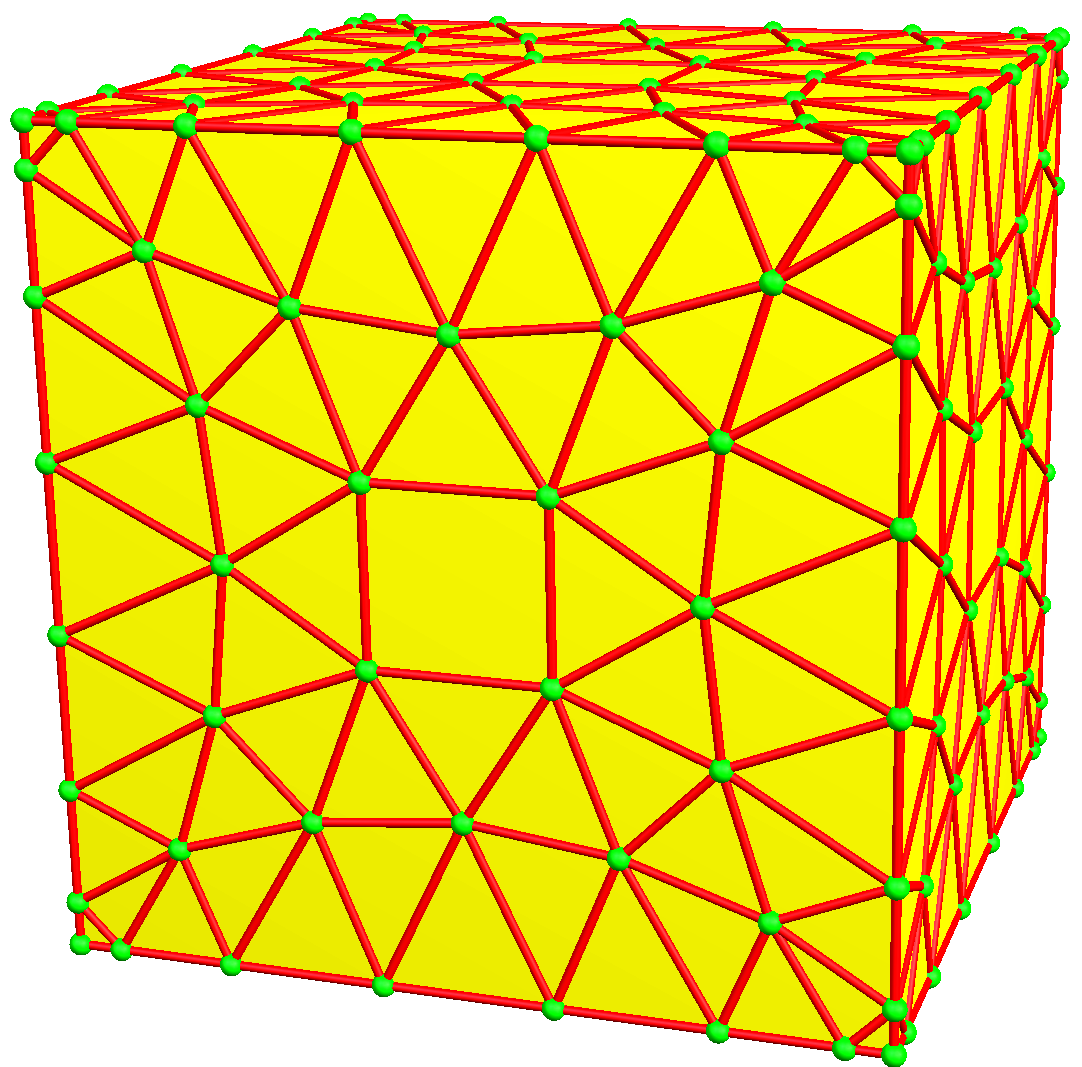 u7 = u2,1u1,2 = vrv | vrvd = dwrw | dvrv = wrwd | c7 = c2,1c1,2 = wrw |
| 8 | 0 | I | 64 |  u8 = u3 | u3d = dc3 | du3 = c3d | c8 = c3 |
| 9 | 0 | I | 81 | 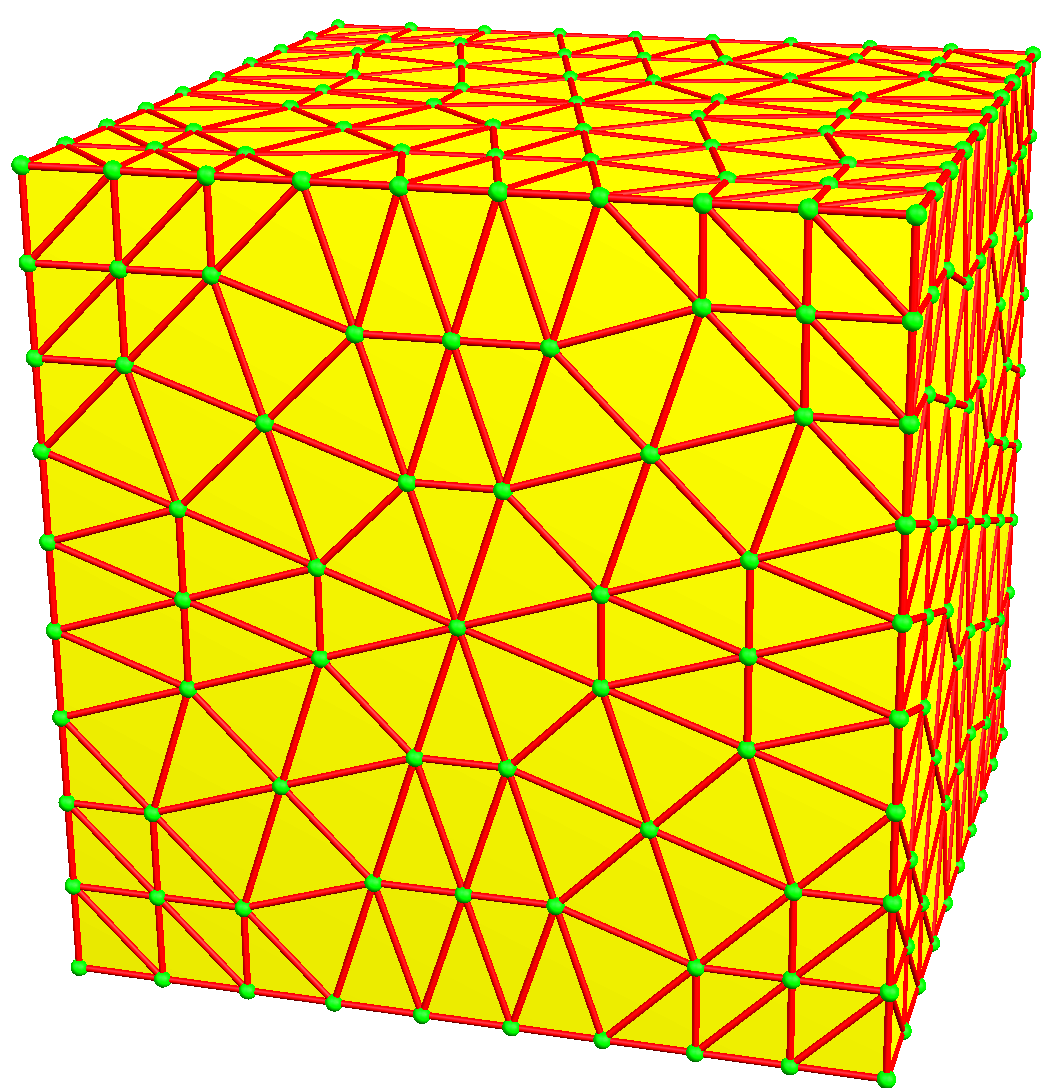 u9 = n4 | n3k = kz3 | tn3 = z3t | c9 = z4 |
| 1 | 1 | II | 3 | -- u1,1 = n | -- k | -- t | -- c1,1 = z |
| 2 | 1 | III | 7 | v = u2,1 | -- vd = dw | dv = wd | -- w = c2,1 |
| 3 | 1 | III | 13 | u3,1 | u3,1d = dc3,1 | du3,1 = c3,1d | 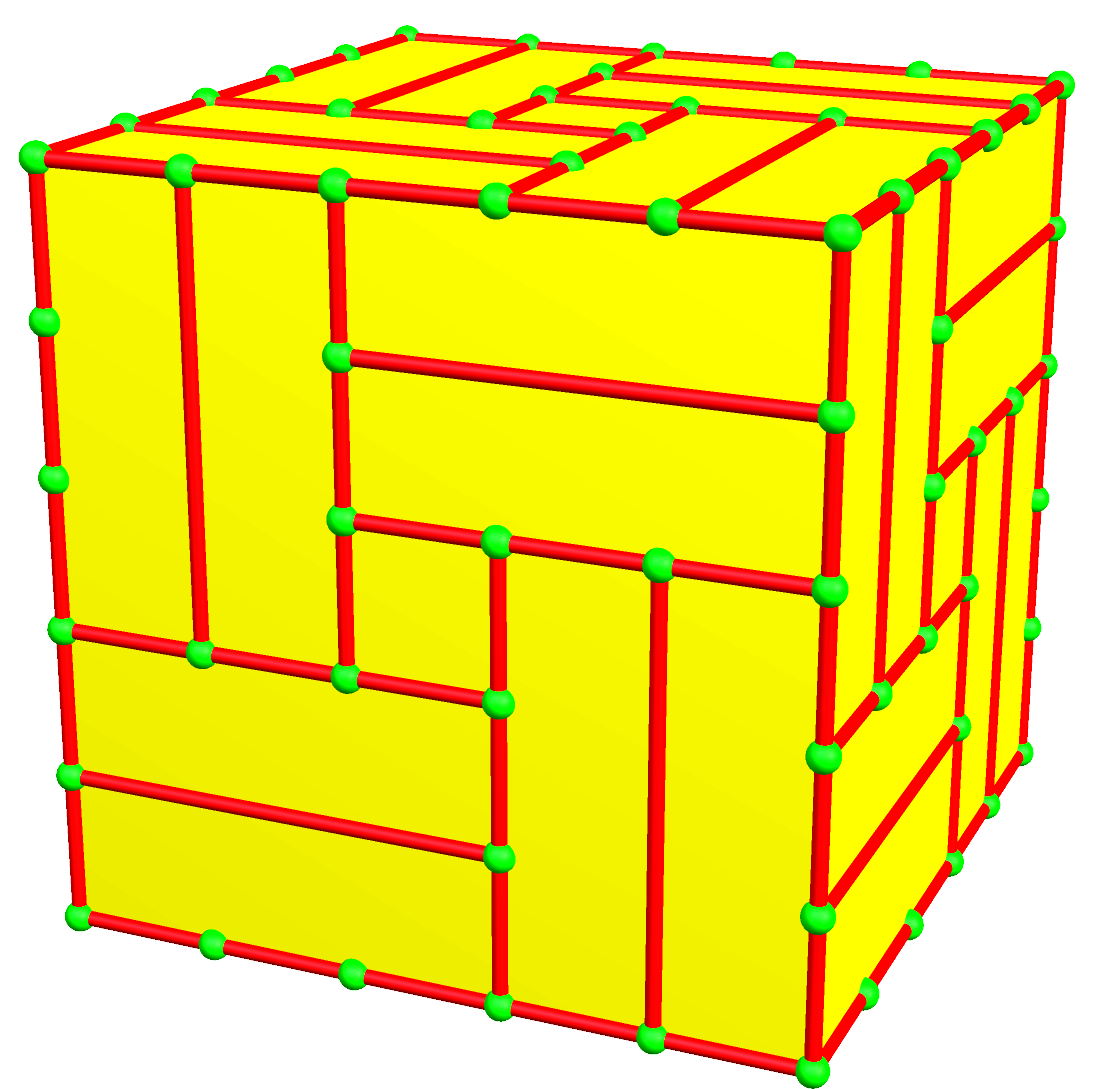 c3,1 |
| 3 | 2 | III | 19 | u3,2 | u3,2d = dc3,2 | du3,2 = c3,2d | 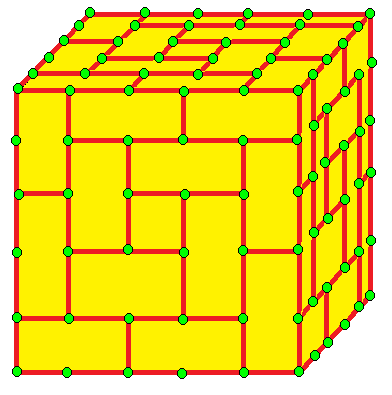 c3,2 |
| 4 | 3 | III | 37 | u4,3 | u4,3d = dc4,3 | du4,3 = c4,3d |  c4,3 |
| 5 | 4 | III | 61 | u5,4 | u5,4d = dc5,4 | du5,4 = c5,4d |  c5,4 |
| 6 | 5 | III | 91 | u6,5 = u1,2u1,3 | u6,5d = dc6,5 | du6,5 = c6,5d |  c6,5=c1,2c1,3 |
| 7 | 6 | III | 127 | u7,6 | u7,6d = dc7,6 | du7,6 = c7,6d |  c7,6 |
| 8 | 7 | III | 169 | u8,7 = u3,12 | u8,7d = dc8,7 | du8,7 = c8,7d | 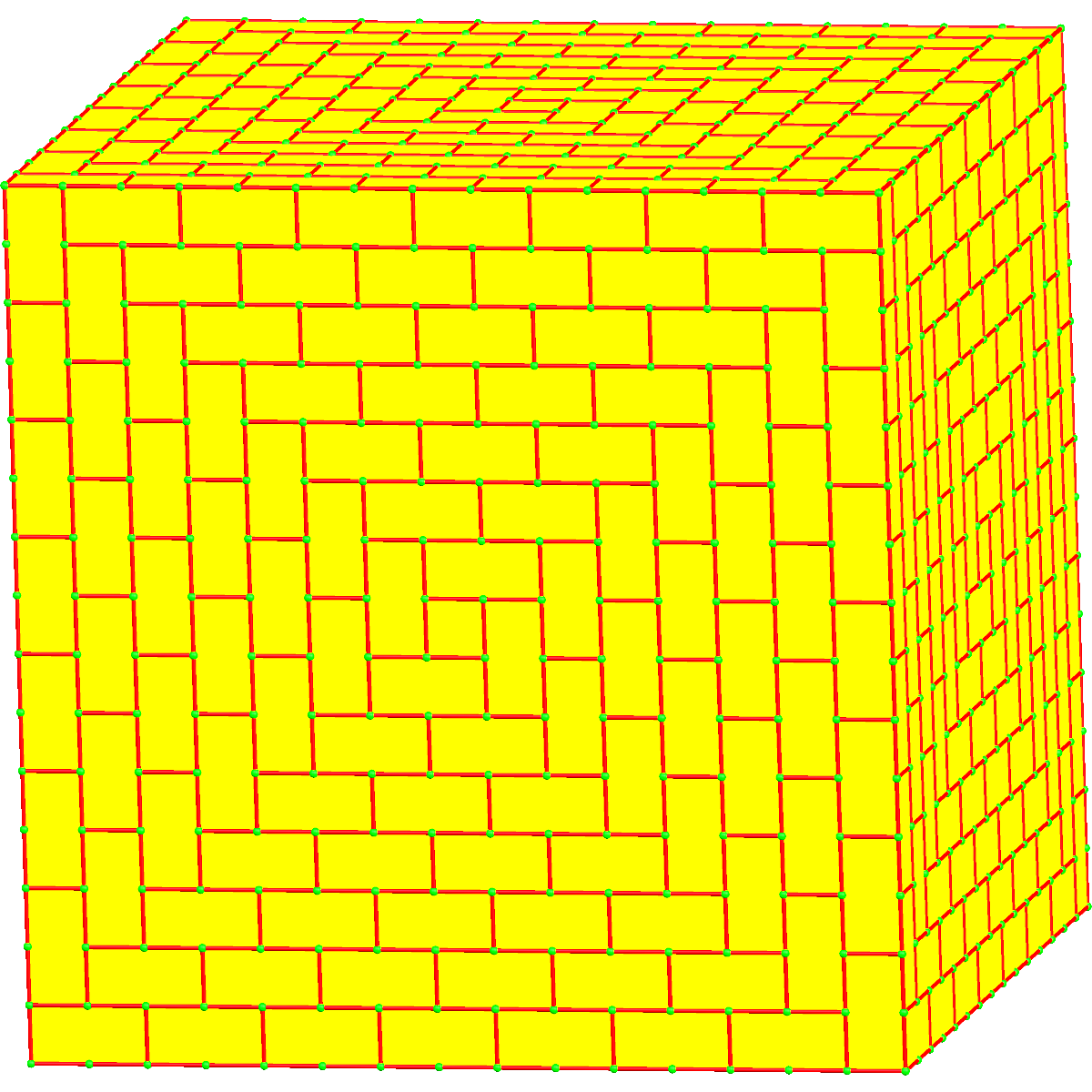 c8,7 = c3,12 |
| 9 | 8 | III | 217 | u9,8 = u2,1u5,1 | u9,8d = dc9,8 | du9,8 = c9,8d |  c9,8 = c2,1c5,1 |
4. 2. 사각형 계열 (Quadrilateral)
사각형 골드버그-콕세터(GC) 계열은 ''ea,b'' 와 ''oa,b'' 두 가지 연산자로 구성된다. 이 연산자들은 두 개의 정수 a, b로 나타내어지며, a와 b는 복소수와 연관되어 특정한 유클리드 영역과의 관계를 가진다. 사각형 GC 계열은 가우스 정수와 연관된다.[1]사각형 GC 연산자는 다음과 같이 세 가지 클래스로 구분된다.
- 클래스 I: 아키랄(achiral)이며, 원래 가장자리를 보존한다. 0 지수는 생략하여 ''ea'' 또는 ''oa'' 와 같이 나타낼 수 있다.
- 클래스 II: 아키랄(achiral)이다.
- 클래스 III: 나머지 모든 연산자들을 포함한다. 키랄(chiral)이며, ''ea,b'' 와 ''eb,a'' 또는 ''oa,b'' 와 ''ob,a'' 는 서로 키랄 쌍이다.
사각형 골드버그-콕세터 연산자의 상세한 정보는 아래 표와 같다.
| a | b | 클래스 | 모서리 계수 T = a2 + b2 | 행렬 | 마스터 사각형 | x | xd | dx | dxd |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | I | 1 |  | |||||
| -- e1 = d | |||||||||
| 2 | 0 | I | 4 |  | -- o2 = o = j2 | -- e2 = e = a2 | |||
| 3 | 0 | I | 9 |  | 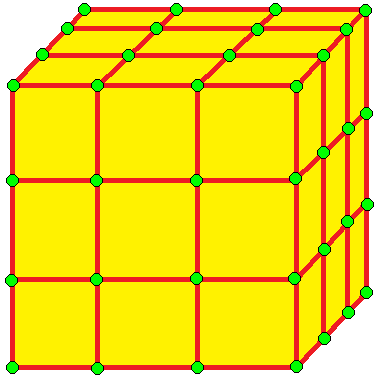 o3 | 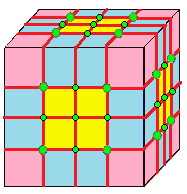 e3 | -- o3 | ||
| 4 | 0 | I | 16 |  | 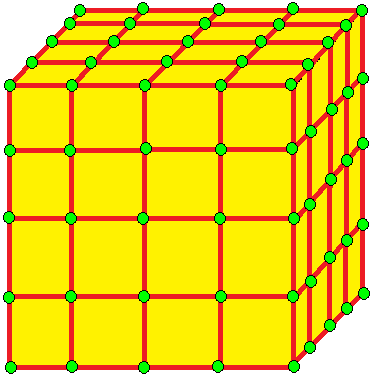 o4 = oo = j4 | 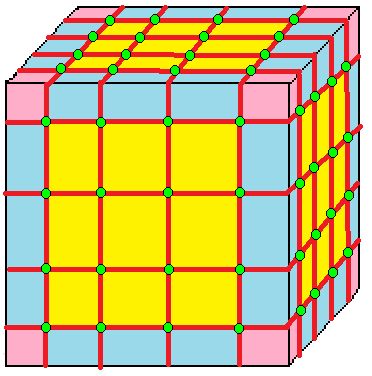 e4 = ee = a4 | |||
| 5 | 0 | I | 25 |  | 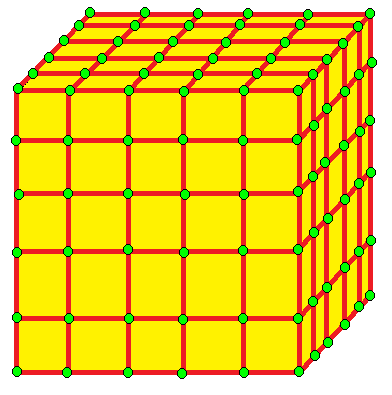 o5 = o2,1o1,2 = prp | e5 = e2,1e1,2 | |||
| 6 | 0 | I | 36 |  | 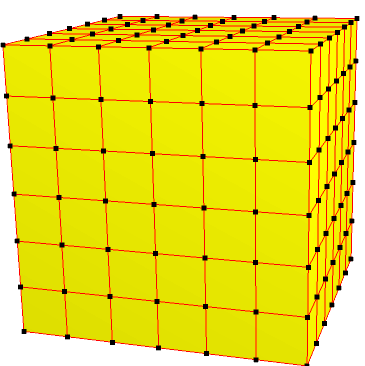 o6 = o2o3 | e6 = e2e3 | |||
| 7 | 0 | I | 49 |  | 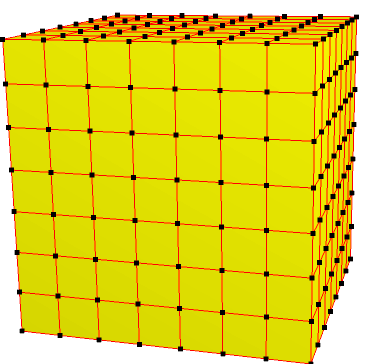 o7 | e7 | |||
| 8 | 0 | I | 64 |  | 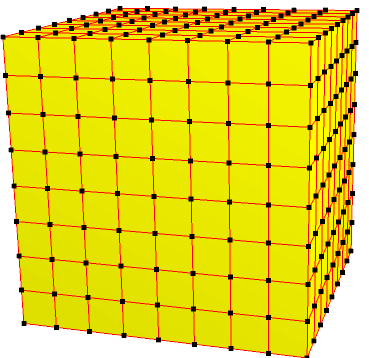 o8 = o3 = j6 | e8 = e3 = a6 | |||
| 9 | 0 | I | 81 |  | 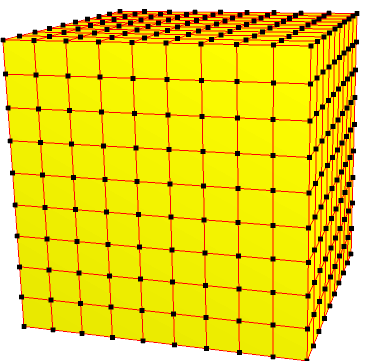 o9 = o32 | e9 = e32 | |||
| 10 | 0 | I | 100 |  | 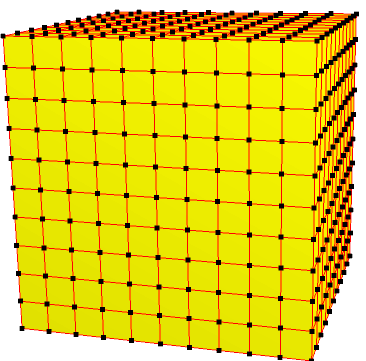 o10 = oo2,1o1,2 | e10 = ee2,1e1,2 | |||
| 1 | 1 | II | 2 |  | -- o1,1 = j | -- e1,1 = a | |||
| 2 | 2 | II | 8 |  | 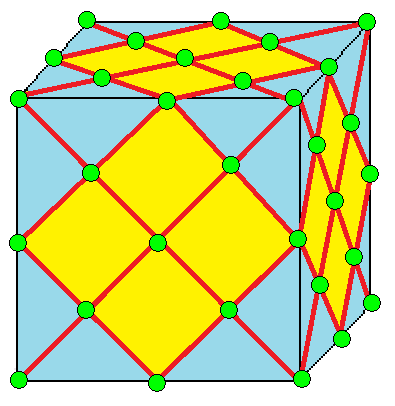 o2,2 = j3 | 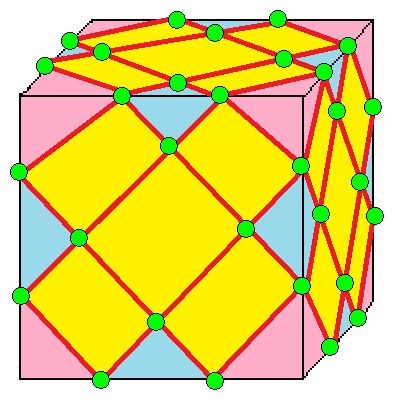 e2,2 = a3 | |||
| 1 | 2 | III | 5 |  | -- o1,2 = p | -- e1,2 = dp = pd | -- p | ||
| I, II, 또는 III | T 짝수 | ... | oa,b | ea,b | |||||
| I 또는 III | T 홀수 | ... | oa,b | ea,b | oa,b | ||||
5. 아르키메데스 다면체와 카탈랑 다면체 생성
콘웨이 다면체 표기법의 기본 연산을 사용하면 정다면체를 씨앗(seed)으로 하여 모든 아르키메데스 다면체와 카탈랑 다면체를 만들 수 있다. 예를 들어, 깎은 정사면체는 tT로, 마름모십이면체는 jC 또는 jO로 표현할 수 있다.
아래는 아르키메데스 다면체와 카탈랑 다면체를 콘웨이 표기법으로 나타낸 것이다.
| 다면체 | 이름 | 콘웨이 표기법 |
|---|---|---|
| -- | 깎은 정사면체 | tT |
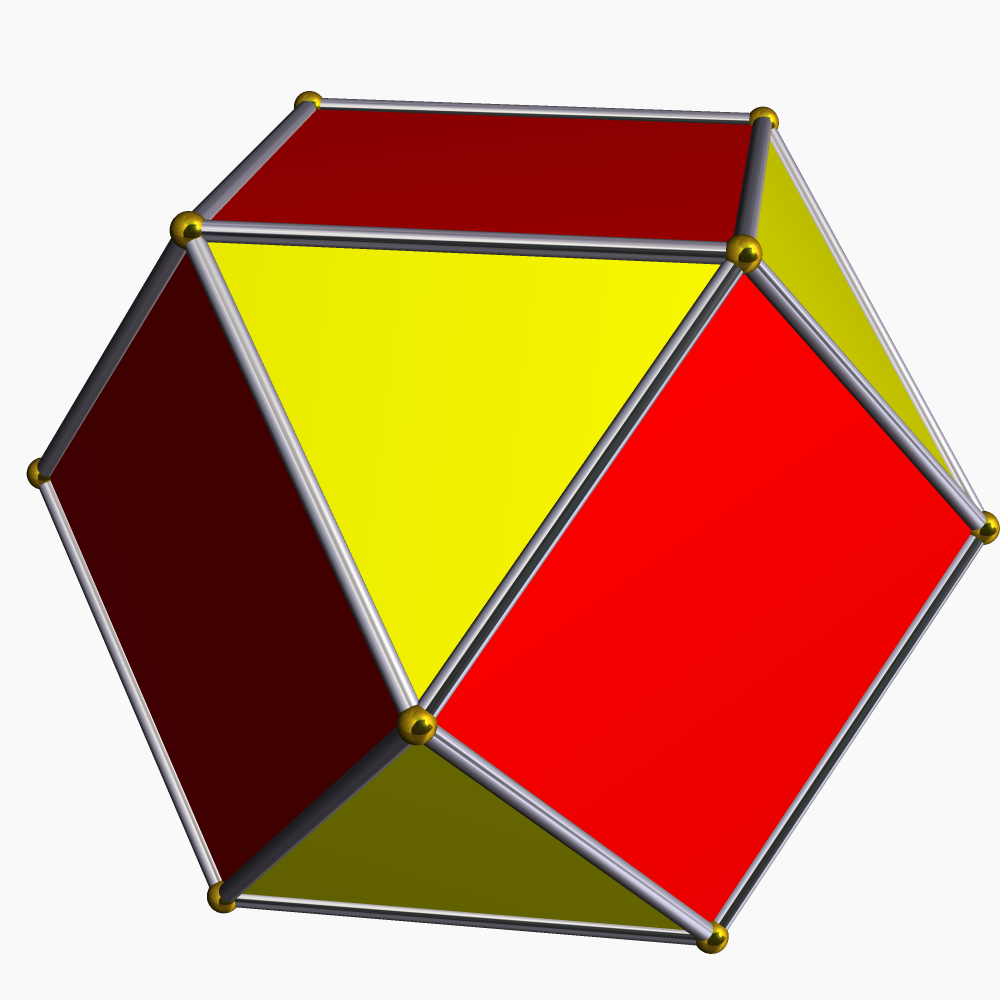 | 정육팔면체 | aC = aaT |
| -- | 깎은 정육면체 | tC |
| -- | 깎은 정팔면체 | tO = bT |
| -- | 마름모육팔면체 | eC = a3T |
| -- | 깎은 정육팔면체 | bC |
| -- | 스너브 정육면체 | sC |
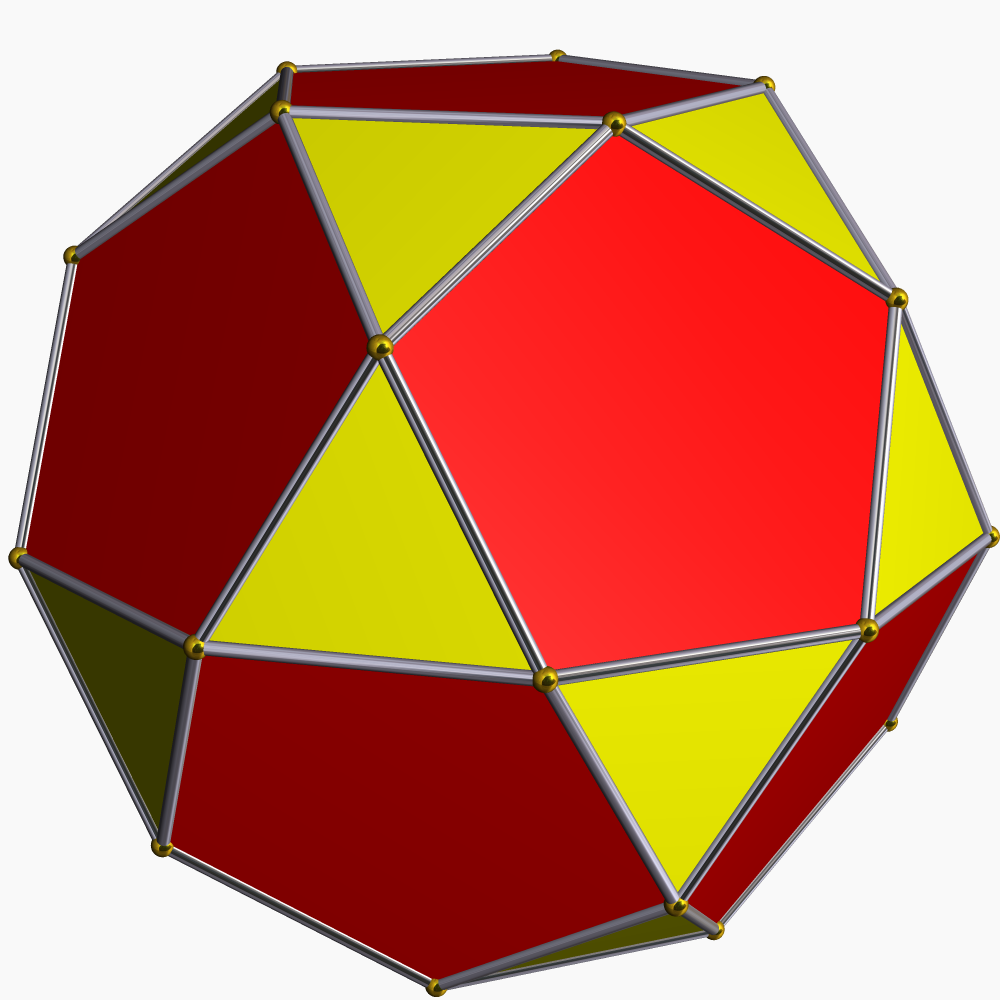 | 이십십이면체 | aD |
| -- | 깎은 정십이면체 | tD |
| -- | 깎은 정이십면체 | tI |
| -- | 마름모이십십이면체 | eD |
| -- | 깎은 정이십십이면체 | bD |
| -- | 스너브 정십이면체 | sD & sI |
| 다면체 | 이름 | 콘웨이 표기법 |
|---|---|---|
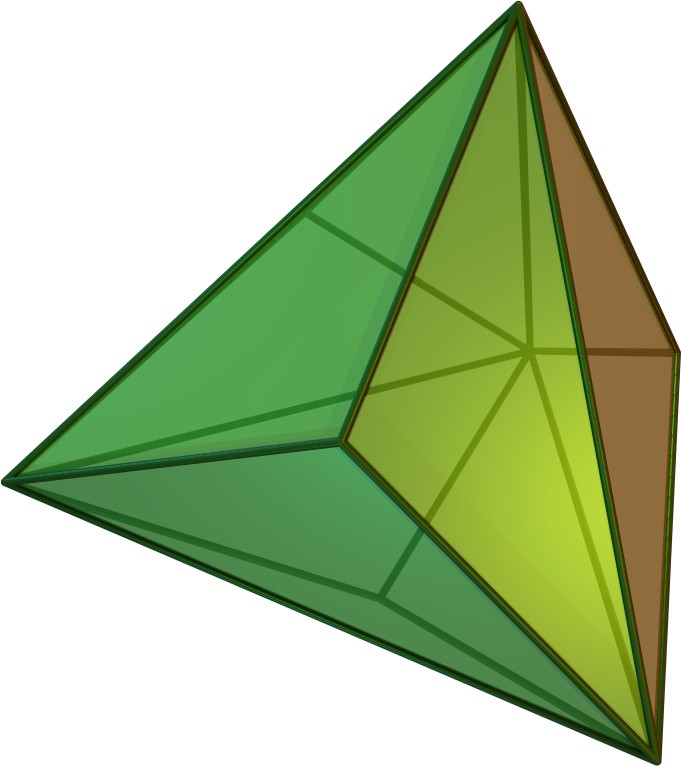 | 삼방사면체 | kT |
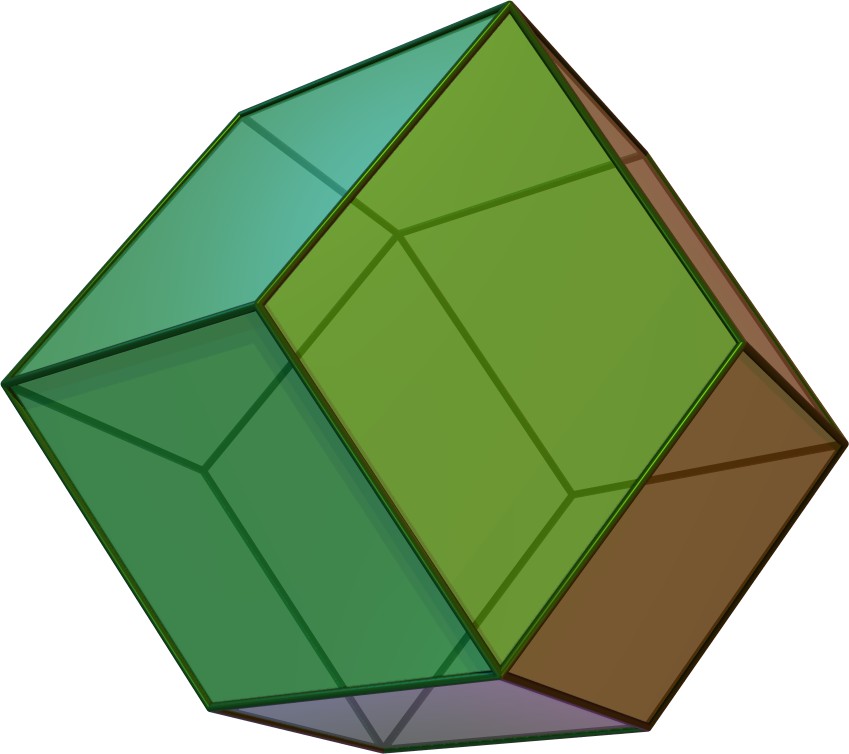 | 마름모십이면체 | jC |
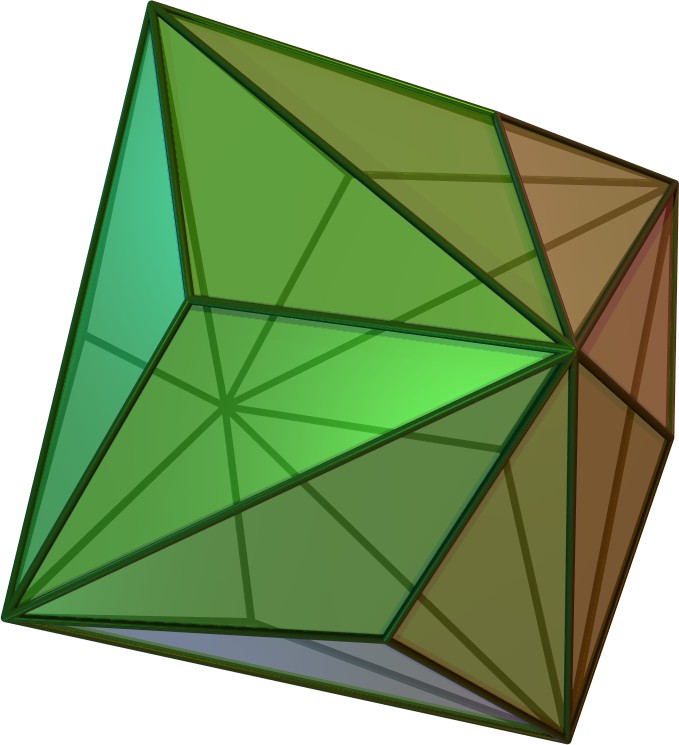 | 삼방팔면체 | kO |
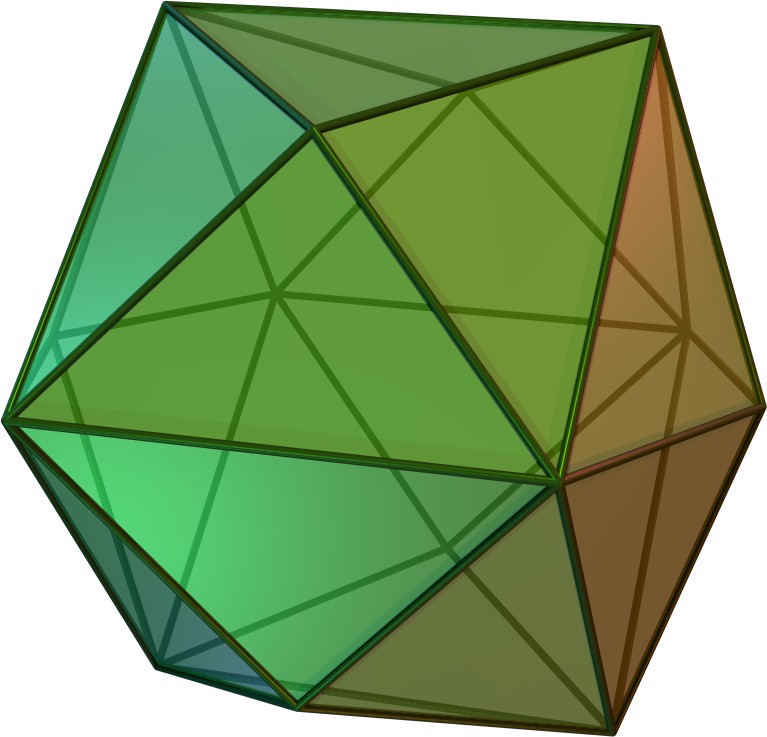 | 사방육면체 | kC |
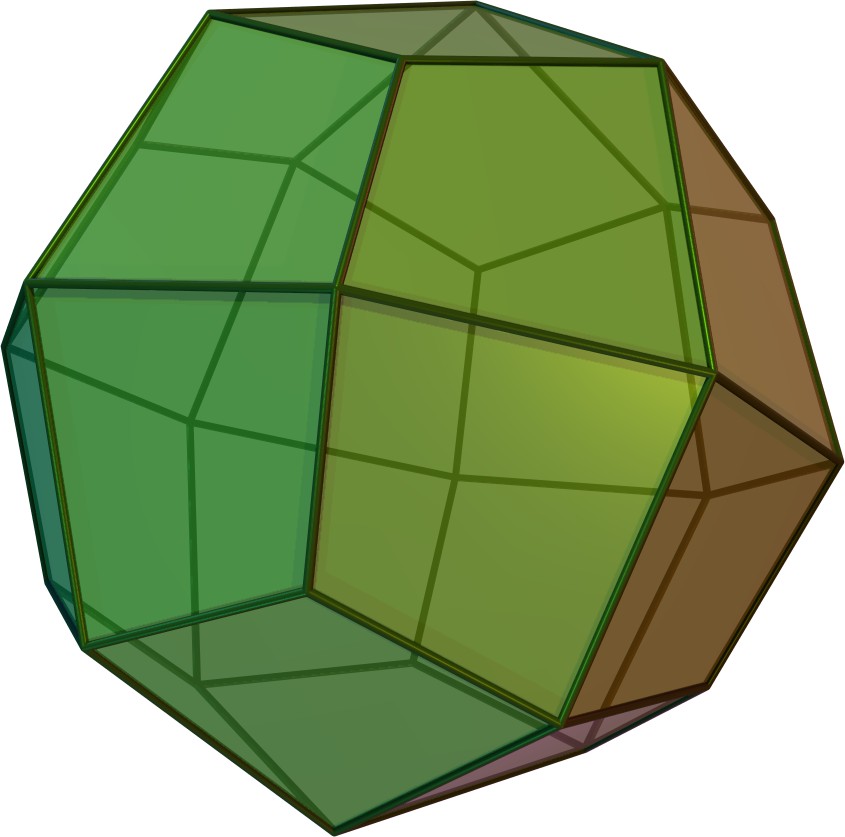 | 델토이드 이십사면체 | oC |
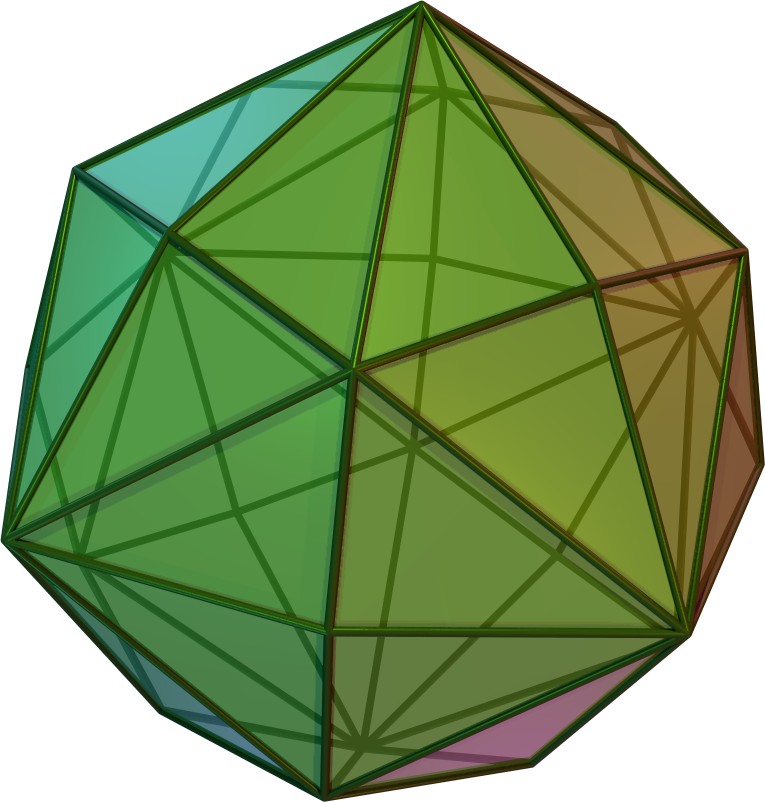 | 육방십이면체 | mC |
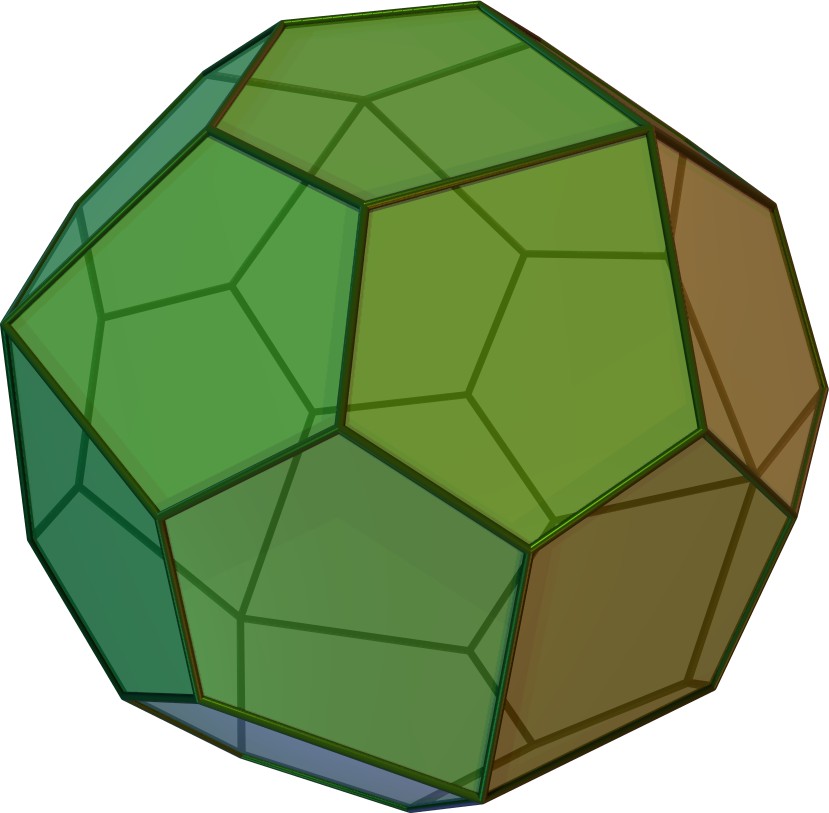 | 오각이십사면체 | gC |
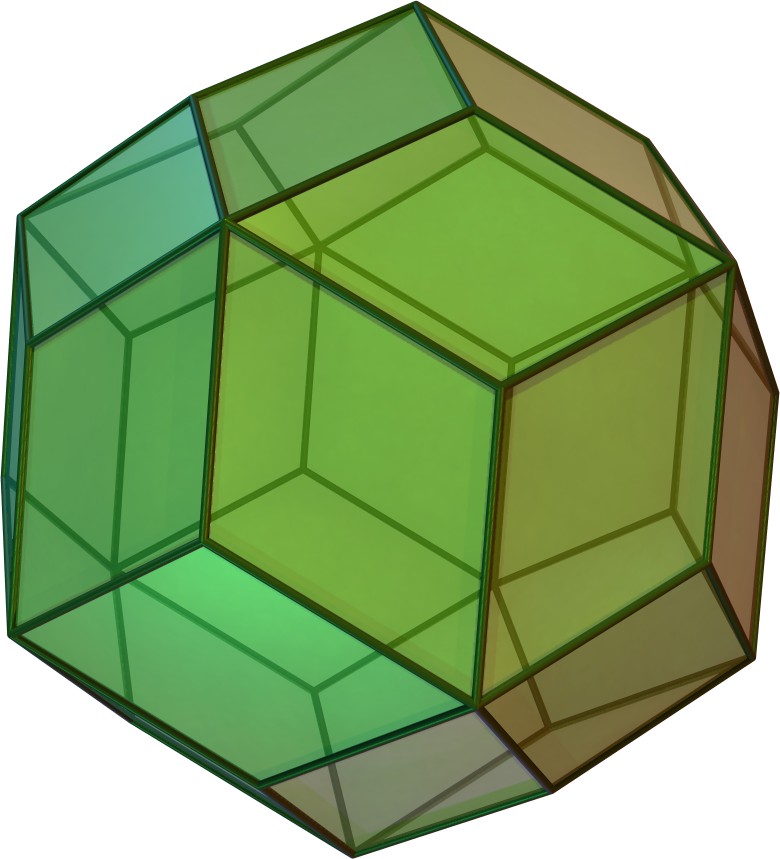 | 마름모삼십면체 | jD |
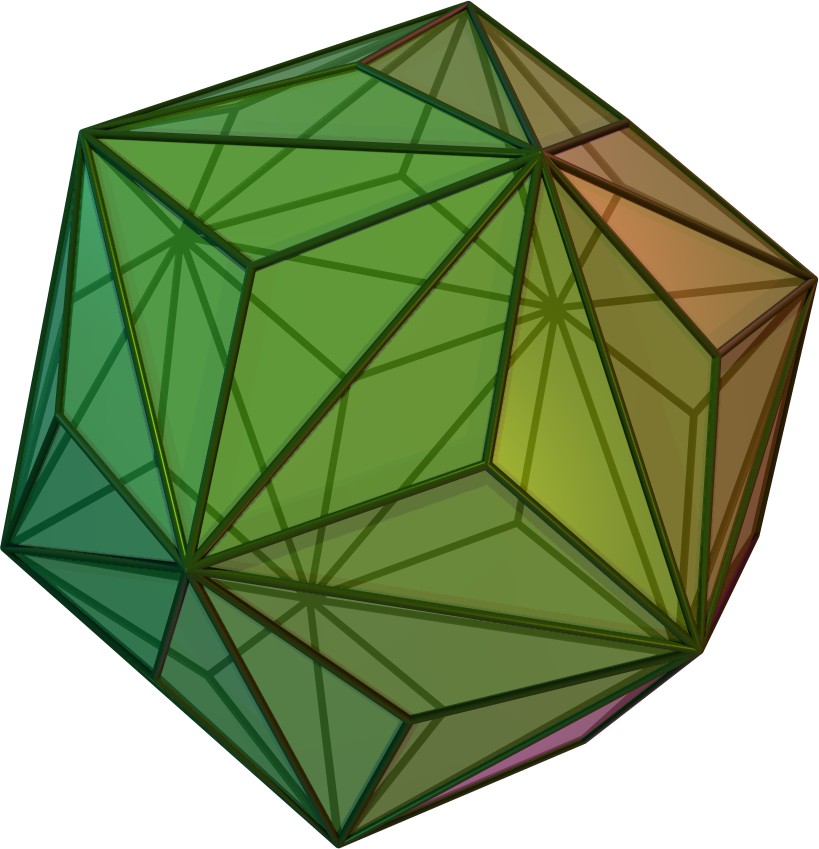 | 삼각이십면체 | kI |
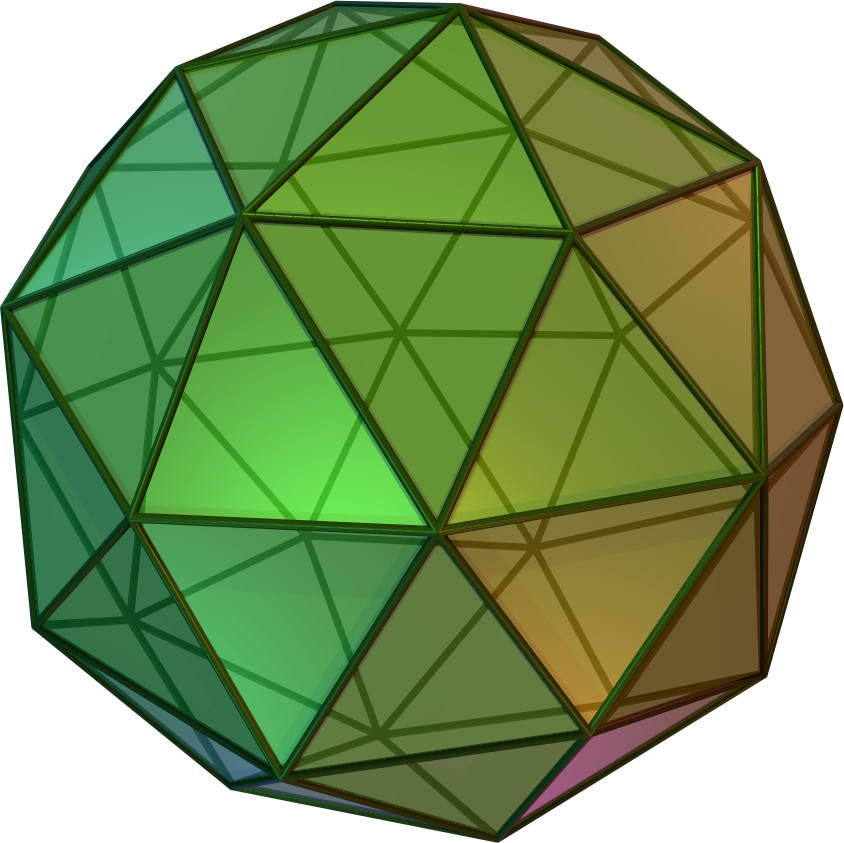 | 오각십이면체 | kD |
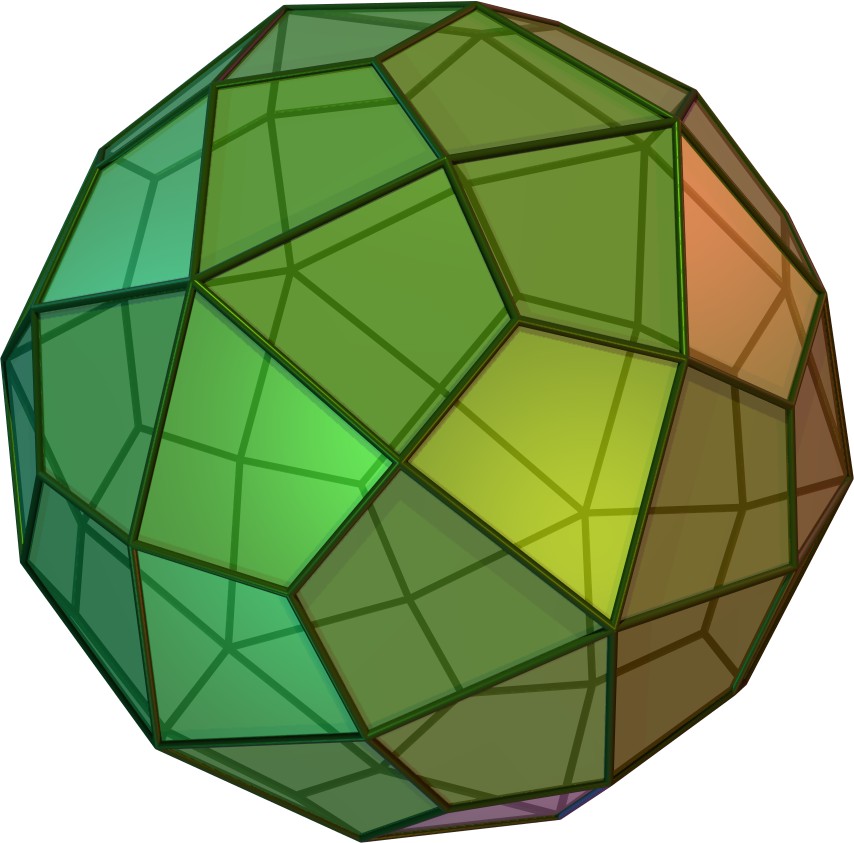 | 델토이드 육십면체 | oD |
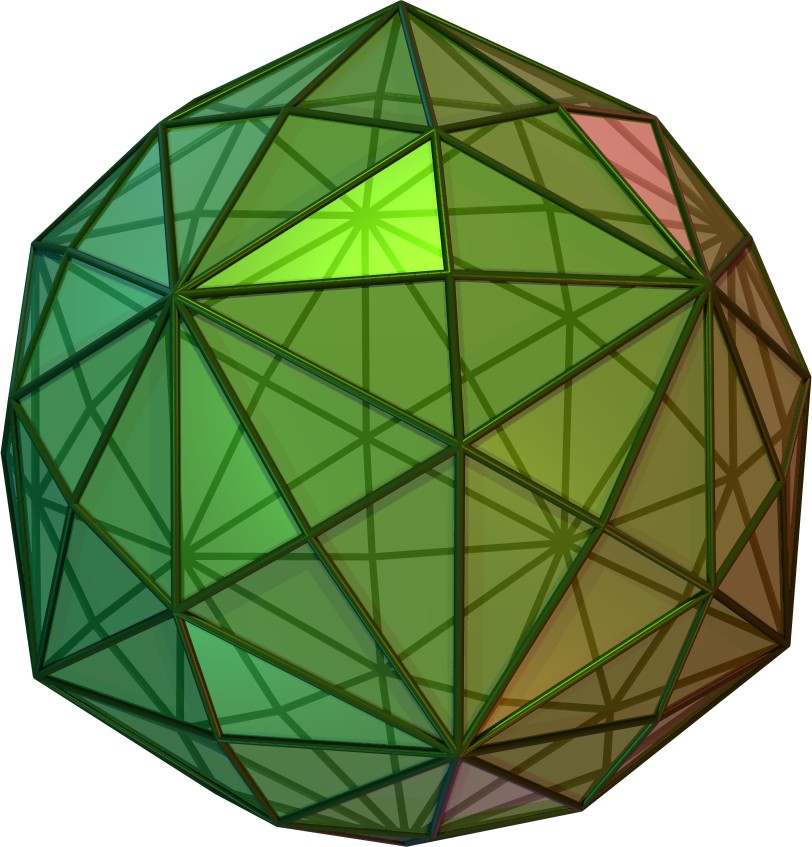 | 육방삼십면체 | mD |
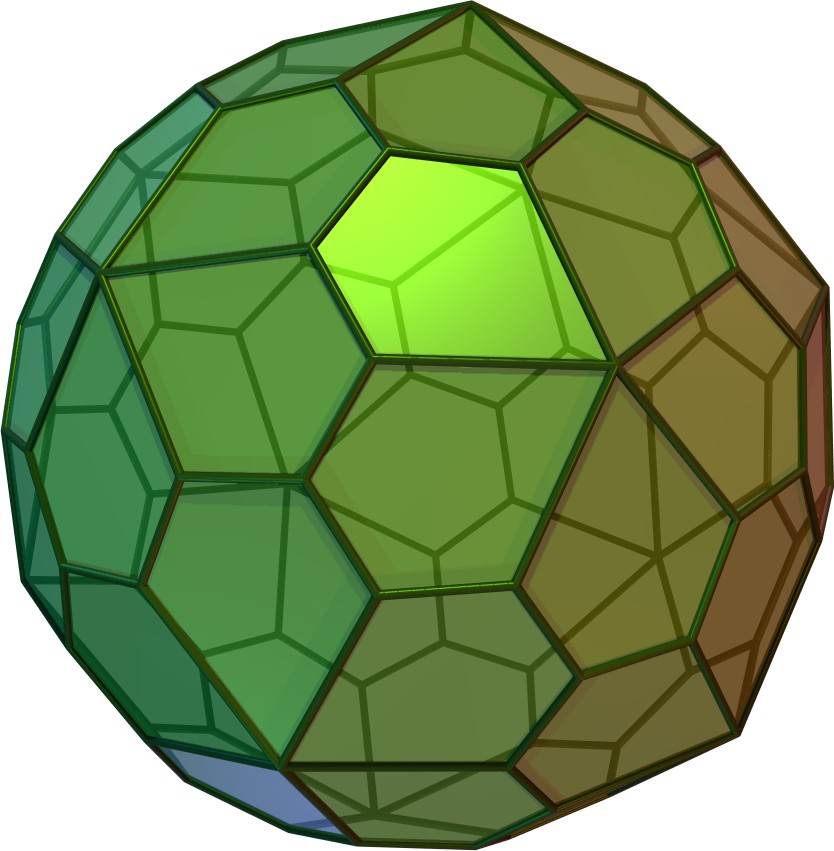 | 오각육십면체 | gD & gI |
6. 생성 예시
콘웨이 다면체 표기법은 다면체를 설명하고 분류하기 위해 고안된 방법이다. 이 표기법은 존 호턴 콘웨이가 개발했으며, 씨앗(seed) 역할을 하는 기본 다면체에서 시작하여 다양한 연산(operations)을 적용하여 복잡한 다면체를 생성하는 방식으로 작동한다.
측지 다면체 및 골드버그 다면체의 목록에서 콘웨이 다면체 표기법을 사용한 예시를 확인할 수 있다.
7. 평면 및 곡면에서의 콘웨이 표기법
콘웨이 표기법은 평면 타일링이나 토러스와 같은 곡면에도 적용할 수 있다.[1]
7. 1. 평면에서의 예시
볼록 정규 테셀레이션과 그 쌍대는 콘웨이 연산자를 정규 테셀레이션 ''Q'', ''H'', ''Δ''에 적용하여 만들 수 있다.



''sQ''

''gQ''



''tH''






''kΔ''



7. 2. 곡면에서의 예시
콘웨이 연산자는 토로이드 다면체와 여러 개의 구멍이 있는 다면체에도 적용될 수 있다.[1]
참조
[1]
서적
The Symmetries of Things
AK Peters
[2]
MathWorld
Conway Polyhedron Notation
[3]
웹사이트
Conway Notation for Polyhedra
http://www.georgehar[...]
1998
[4]
웹사이트
conway - Conway Notation transformations
http://www.antiprism[...]
[5]
웹사이트
polyHédronisme
https://levskaya.git[...]
[6]
웹사이트
Conway Notation for Polyhedra
http://www.georgehar[...]
1998
[7]
간행물
Goldberg, Fuller, Caspar, Klug and Coxeter and a general approach to local symmetry-preserving operations
[8]
arXiv
Generation of Local Symmetry-Preserving Operations
2020-04-12
[9]
arXiv
Local Orientation-Preserving Symmetry Preserving Operations on Polyhedra
2020-04-11
[10]
MathWorld
Rectification
[11]
MathWorld
Cumulation
[12]
MathWorld
Truncation
[13]
웹사이트
Antiprism - Chirality issue in conway
https://groups.googl[...]
[14]
간행물
Generation of an icosahedron by the intersection of five tetrahedra: geometrical and crystallographic features of the intermediate polyhedra
http://www.mi.sanu.a[...]
[15]
conference
Sculpture based on Propellorized Polyhedra
http://www.georgehar[...]
2000-08
[16]
간행물
Goldberg–Coxeter constructions for 3-and 4-valent plane graphs
http://www.combinato[...]
[17]
서적
Geometric Structure of Chemistry-Relevant Graphs: Zigzags and Central Circuits
Springer
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com